
Aberrations chromatiques
Supposons une lentille biconvexe et un rayon incident de lumière blanche parallèle à l’axe. Localement, à la hauteur d’incidence, la lentille peut être assimilée à un prisme. Ce prisme disperse la lumière, son indice de réfraction variant en raison inverse de la longueur d’onde. La lumière bleue subit une déviation plus grande que la lumière rouge et les rayons émergents coupent l’axe optique en des foyers images différents, le foyer bleu étant plus proche de la lentille que le foyer rouge. Ce résultat caractérise le chromatisme longitudinal de la lentille.

Le même type d’analogie peut s’appliquer pour construire l’image d’un objet en considérant le rayon issu du point hors d’axe parallèle à l’axe optique et le rayon passant par le centre optique de la lentille pour lequel elle est assimilable à une lame à faces parallèles entraînant une déviation dépendant de la longueur d’onde.

Les images ne se forment pas dans le même plan (aberration longitudinale) et sont de grandeurs différentes, ce qui traduit l’existence d’un chromatisme latéral ou de grandeur.
Aberrations géométriques
Quand les rayons lumineux incidents sont
fortement inclinés sur l'axe optique, les hypothèses de l'approximation de Gauss
ne sont plus valables. Ainsi à chaque point du plan objet ne peut correspondre
un point unique du plan image, c'est-à-dire que, à une onde sphérique S supposée
émise en un point B du plan objet, ne peut correspondre une onde émergente
sphérique S' centrée sur l'image de Gauss B', mais une onde déformée
![]() '
dont l'écart
'
dont l'écart ![]() par
rapport à l'onde sphérique idéale traduit l'existence d'une aberration
géométrique.
par
rapport à l'onde sphérique idéale traduit l'existence d'une aberration
géométrique.
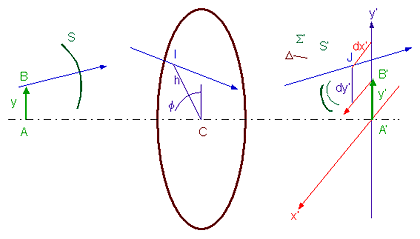
Nous notons aussi que le rayon lumineux issu du
point B ne passe pas par l’image de Gauss B' mais traverse le plan de cette
image en un point J dont les coordonnées dx' et dy' définissent l’aberration
transversale. Ces grandeurs dérivent de l’expression du chemin optique aberrant
et sont donc d’un degré moindre. Leurs termes sont d’ordre impair par rapport à
hy', les termes du premier degré proportionnels à h ou y' étant nuls, l’origine
des coordonnées de l’aberration transversale étant prises en B' image de Gauss.
Les premiers termes illustrent les aberrations dites du troisième ordre.
Considérons une lentille de grand diamètre et un point objet
situé sur l’axe à l'infini émettant un faisceau de lumière monochromatique. Les
rayons parallèles à l’axe attaquent la lentille sous des angles d’incidence
différents en des points où celle-ci peut être assimilée à des prismes d’angles
d’autant plus grands que l’incidence est élevée. Les rayons émergents sont donc
d’autant plus déviés et ne convergent pas en un même point. Ils remplissent un
domaine de l’espace enfermé par une surface de révolution concentrant une grande
partie de l’énergie, une autre concentration s’observant sur un segment de l’axe
optique correspondant à l’ensemble des foyers. Ces deux nappes, respectivement
dénommées tangentielle et sagittale, constituent la caustique d’aberration
sphérique.
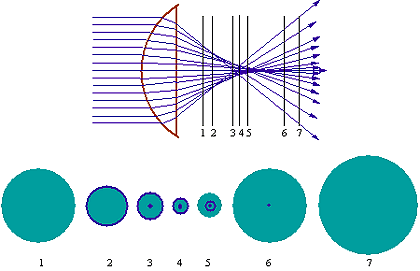
La section du faisceau lumineux par un plan
perpendiculaire à l’axe montre l’allure de l’image du point objet en fonction de
la position sur l’axe.
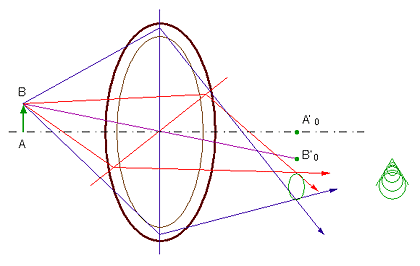
Supposons maintenant un système optique, constitué de
plusieurs lentilles afin d’être corrigé de l’aberration sphérique, formant
l’image d’un point B situé à une faible distance de l’axe, diaphragmé par une
ouverture annulaire. Si un rayon lumineux issu de B décrit cet anneau, on
constate que son intersection avec le plan image décrit un cercle avec une
vitesse double. Pour des anneaux de diamètres différents, ces cercles sont
différents mais restent tangents à deux segments passant par l’image B'0
obtenue si le système était de faible ouverture (image de Gauss ou paraxiale).
Cette tache, image d’un point hors de l’axe traduit l’existence de l’aberration
de coma ou d’aigrette.
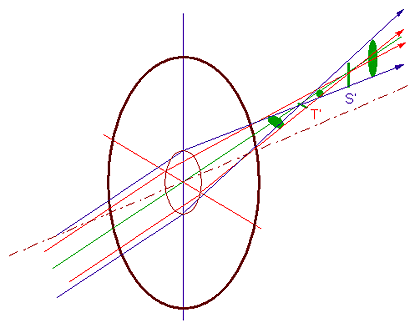
Supposons maintenant que le système optique
fournisse l’image d’un point fortement éloigné de l’axe. Après traversée du
système, un pinceau étroit de rayons incidents ne converge pas en un point mais
s’appuie sur deux petits segments de droite respectivement perpendiculaire au
plan de figure et dans ce plan appelés focales tangentielle
et sagittale.
Cette aberration caractérise l’astigmatisme.
Si l’on décrit tout le champ, c’est-à-dire si l’on considère
des pinceaux incidents différemment inclinés, ces focales engendrent des
surfaces (tangentielle et sagittale) de révolution autour de l’axe optique
tangentes en leur sommet, caractérisant la courbure de champ.
Enfin, si l’on associe à une lentille un diaphragme non situé dans son plan et que l’on forme l’image d’un quadrillage régulier, on constate que celle-ci est déformée en barillet ou en coussinet ou croissant, traduisant l’existence de distorsion.

L’aspect réel de ces aberrations n’est pas toujours évident. Pour un système de grande ouverture et à grand champ leurs effets se superposent (sans compter l’influence des ordres supérieurs). Néanmoins avec quelques précautions leur mise en évidence expérimentale peut être obtenue.