Structure des Naines Blanches
Les naines blanches sont des étoiles en fin de vie qui ont brûlé leur
carburant dhydrogène qui entretenait la combustion thermonucléaire. Cette
dernière produisait de lénergie qui contrebalançait leffondrement de
létoile sous son propre poids.
Le but de ce travail est tout dabord dexaminer le comportement dun gaz
délectrons subissant des pressions gigantesques puis détablir une relation
entre la masse et le rayon dune naine blanche à léquilibre. Enfin, nous
étudierons la validité du modèle des étoiles polytropes appliqué au cas des
naines blanches.
I - Gaz dégénéré délectrons et calcul de la pression
1)Gaz dégénéré délectrons
Nous étudions un gaz délectrons sans interaction qui obéit donc à la
statistique de Fermi-Dirac. Le nombre moyen doccupation sécrit
alors :

avec

De manière numérique, nous pouvons simuler lévolution de lallure du
facteur de Fermi en fonction de lénergie e et de la
température T. Pour cela, on suppose pour simplifier que la constante de
Boltzmann kB=1 et que le potentiel chimique m =2 (on note que celui-ci est dan labsolu fonction de la
température). Ainsi, nous pouvons écrire le petit programme suivant sous
Matlabä :
clear all;kb=1; % Constante de Boltzmann
mu=2; % Potentiel
Chimique
T=0.001:0.001:1; % " Gradient " de température pour le
programme
for
j=1:length(T)
beta(j)=1/(kb*T(j));
epsilon=0.1:0.1:4;
for
i=1:length(epsilon)
Nf(i,j)=1/(exp(beta(j)*(epsilon(i)-mu))+1); %
Nb(epsilon,beta) moyen de fermions au
end % niveau d'énergie
epsilon
plot(epsilon,Nf(:,j));
text(2.5,0.6,sprintf('T=
%1.3f',T(j)));
pause(0)
end
Nous obtenons alors, en unité arbitraire, la figure suivante :

Figure 1
Quand T® 0, la fonction de Fermi devient une
" marche " (ou fonction dHeavyside) à savoir :

De manière générale, le nombre total délectrons peut sécrire :


A basse température, comme nous lavons vu précédemment on peut simplifier
lintégrale :


On définit la température de Fermi : 
Application Numérique pour les Naines Blanches :
S=1/2
NA=6,02.1023


h=6,63.10-34Js-1
me=9,11.10-31Kg

ainsi

Exploitation du résultat :
On estime la température de cur dune naine blanche autour de
107 K. En prenant comme hypothèse que le gaz délectrons évolue à
température nulle, le rapport
 . Ce
qui signifie que les niveaux dénergie accessibles aux électrons sont en deçà
du niveau de Fermi, par conséquent le gaz est totalement dégénéré et remplit
tous les niveaux jusquà e F.
. Ce
qui signifie que les niveaux dénergie accessibles aux électrons sont en deçà
du niveau de Fermi, par conséquent le gaz est totalement dégénéré et remplit
tous les niveaux jusquà e F.
Lapproximation de température nulle est donc une bonne approximation pour
calculer le niveau de Fermi. La fonction de distribution du nombre délectrons
par énergie peut donc se modéliser par une fonction " marche " ou
une fonction dHeavyside.
2)Calcul de la pression quantique
Daprès la statistique de Fermi-Dirac, la fonction de partition généralisée
du système sécrit :

Il sagit ici de fermions donc  = 0
ou 1.
= 0
ou 1.

Or

Ainsi :

Dans le formalisme grand canonique, Le grand potentiel J sécrit :

Dans lapproximation continue, léquation devient :

Dans lespace des impulsions, le nombre délectrons sécrit :

Ainsi

Cette équation peut sintégrer par parties :
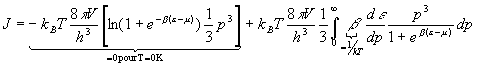
Lénergie relativiste sexprime sous la forme :

Doù :

Si maintenant on se place à température nulle, le premier terme qui est
facteur de la température sannule, la fonction de Fermi NF vaut
lunité comme on la vu au paragraphe précédent et lon nintègre que jusquà
pF. Par conséquent il vient :

Enfin la pression quantique électronique peut donc sécrire :

Si on pose :


On trouve finalement que :

En reprenant les expressions de la densité on a :

Effectuons le changement de variable suivant :

Notre pression devient donc :

Il faut linéariser le sinus hyperbolique :

Lintégrale se réécrit donc :


On respire un grand coup et on rechange de variable
 :
:




Finalement, la pression quantique peut se mettre sous la forme :
(x = xF)

II - Relation masse-rayon
Léquation fondamentale de lastrophysique Newtonienne pour un corps
sphérique de masse M et de rayon R sécrit :

La variation élémentaire de lénergie en fonction du rayon donne
donc :

La variation de cette énergie équivaut pour un gaz parfait au travail de la
pression par rapport au volume soit :

La condition déquilibre prise ici est que la pression due à lexclusion
dun même état quantique (principe de Pauli) est contrebalancée par la
pression due à leffondrement gravitationnel de létoile sous son propre
poids. Ainsi on peut écrire :

Or :

Ainsi, en fonction du rayon r, on obtient léquation suivante :

Effectuons le changement de variable suivant :

Reprenons léquation de lastrophysique en y introduisant la formulation
intégrale de la pression quantique vue au paragraphe précédent, on a
alors :
On pose :

Ainsi notre équation sécrit plus simplement :



Finalement, on arrive à léquation suivante :

La masse dune sphère en fonction de son rayon et de sa densité sécrit
 ainsi :
ainsi :

La résolution de léquation précédente va nous donner des couples de
valeurs
 qui
sont reliés au couples (M,R)m en fonction de x. Il va
nous falloir faire varier le paramètre initial x0 et relever les
valeurs de lintégration x variant de x0 à 0.
qui
sont reliés au couples (M,R)m en fonction de x. Il va
nous falloir faire varier le paramètre initial x0 et relever les
valeurs de lintégration x variant de x0 à 0.
Simulation numérique :
Le logiciel Matlabä possède ses propres routines
de résolution déquations différentielles (ODE, méthode Runge-Kutta).
Seulement, il ne peut résoudre que les équations du premier ordre, il nous
faut donc découpler notre équation du second ordre en un système de deux
équations du premier ordre, pour cela posons :

Ainsi nous obtenons le système :

Reste à introduire les relation de masse et rayon que lon défini
précédemment, posons par exemple :

Programme principal en langage Matlabä
:
clear all;
format long;
c = 299792458.0;
hb =
1.05457266e-34;
mp = 1.6726231e-27;
me = 9.1093897e-31;
G =
6.67259e-11;
Ms = 1.989e30;
Rs = 6.9599e8;
mu=2;
m0 = sqrt( 3.0 *
pi * ( ( hb * c / G ) ^ 3 ) ) / ( 2.0 * mp * mp * mu * mu);
r0 = mu * sqrt(
3.0 * pi * ( hb ^ 3 ) / ( G * c ) ) / ( 2.0 * mp * me );
for
i=1:61
j=(i-31)/10;
t0=1e-100;
tf=100;
x0=[10^j 0 0 0];
tspan=[t0 tf];
[y,x]=ODE45('fode',tspan,x0);
yf=0;
while
(x(yf+1,1) >= 0) & (yf+1 < length(x(:,1))) % x(1)=0 fin de
lintégration
yf=yf+1;
end
r(i)= x(yf,4) * r0 /Rs;
m(i)= x(yf,3) *
m0 /Ms;
end
semilogy(m,r);
Et la fonction appelée par la routine dintégration ODE45 :
function dx=fode(t,x)
dx = [ x(2)
-( 2*x(2)/t +
x(2)^2/(x(1)*(x(1)^2+1)) + x(1)^2*sqrt(x(1)^2+1) )
t^2 *
x(1)^3
1];
Pour différentes valeurs de m = A/Z nous obtenons
les courbes suivantes :

Figure 2
Il apparaît donc une masse limite dite masse de Chandrasekhar (MCh
@ 1.44 M pour
m = 2) quand le rayon diminue. Ceci est du au fait
que le principe dexclusion de Pauli (pris comme hypothèse pour les calculs)
ne permet pas que deux fermions (électrons) puissent se rapprocher infiniment
lun de lautre (en dautres termes avoir le même état quantique). Ainsi une
naine blanche, qui nest pas une étoile dégénérée (comme une étoile à
neutrons), voit son rayon lié à sa masse en fonction de sa composition
(rapport Z/A) avec toutefois une limite, i.e. une étoile ne pourra devenir une
naine blanche que si sa masse est inférieure MCh. Au delà, nous
aurons affaire à des étoiles à neutrons ou à des trous-noirs.
Enfin, la connaissance de deux paramètres entre rayon, masse et composition
nous permet de déduire le troisième. Ainsi, Sirius B dont la composition doit
être connue par analyse spectroscopique et la masse par analyse de son
mouvement gravitationnel dans le repère galactique, a un rayon à peu près
10-1 à 10-2 fois plus petit que le
soleil.
III - Validité de lapproximation des étoiles polytropes
Lapproximation des étoiles polytropes consiste à dire que la pression et
la densité sont reliées par une pure loi de puissance :

Où K et g sont des constantes.
Si on reporte cette relation dans la formule qui relie la pression en
fonction du rayon pour un système sphérique homogène on obtient :

Les conditions aux limites nous donne :

Effectuons le changement de variable suivant :

Notre équation peut alors être mise sous la forme dite de Lane
Emden :

Cette équation peut être résolue exactement de manière analytique.
Cependant, nous pouvons approximer dans les deux cas extrêmes des particules
relativistes où non.
Considérons un volume V contenant N particules. Alors, lénergie totale E
est donnée par la règle "  par
degré de liberté " soit :
par
degré de liberté " soit :
 (ainsi pour un gaz monoatomique évoluant dans lespace à trois
dimensions, a = 3 ).
(ainsi pour un gaz monoatomique évoluant dans lespace à trois
dimensions, a = 3 ).
La loi des gaz parfaits ne fait intervenir que la densité de
particules :

Doù la relation :

Supposons maintenant que dans le cas général (hors gaz parfaits) on
ait :
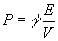
Si lon compresse un gaz de manière adiabatique ( i.e. en ne considérant
pas les phénomènes thermiques ce qui est le cas ici puisquon a dit quune
naine blanche avait épuisé tout son carburant dhydrogène ) le premier
principe de la thermodynamique (conservation de lénergie) nous dit
que :
 où E
est lénergie, P la pression et V le volume.
où E
est lénergie, P la pression et V le volume.
Ainsi :

Lintégration donne :

Or si on injecte ce résultat dans notre équation polytropique on
obtient :
g
= g - 1
et donc :

Reste à exprimer cette relation dans le formalisme de
Fermi-Dirac :

Deux cas extrêmes se présentent ici à savoir lénergie dune électron est
elle relativiste ou non. Dans le cas non relativiste, on peut
écrire :

Soit :
 (électrons non relativistes)
(électrons non relativistes)
Pour le cas des électrons ultra relativistes on a
 et
donc :
et
donc :

Soit :
 (électrons ultra relativistes)
(électrons ultra relativistes)
Reprenons maintenant lexpression de la pression quantique trouvée au
premier paragraphe :
 avec
avec

Dans les deux cas, on peut donc exprimer
 :
:

La simulation numérique nous donne les résultats suivants :

Figure 3
Il apparaît donc que les deux cas extrêmes délimitent le domaine de
variation pour g . Quand la densité devient de
lordre de plusieurs
 ,
g diverge fortement et ce que lon considère les
électrons relativistes ou pas. Lapproximation polytropique ne convient plus
alors. La pression (en puissance de g pour un
polytrope) augmenterait infiniment. On se rend compte ainsi intuitivement
quil existe donc une limite à ne pas dépasser, limite qui conduit à la masse
de Chandrasekhar comme on la vu précédemment.
,
g diverge fortement et ce que lon considère les
électrons relativistes ou pas. Lapproximation polytropique ne convient plus
alors. La pression (en puissance de g pour un
polytrope) augmenterait infiniment. On se rend compte ainsi intuitivement
quil existe donc une limite à ne pas dépasser, limite qui conduit à la masse
de Chandrasekhar comme on la vu précédemment.
Les naines blanches ayant une densité de lordre de
106g.cm-3 peuvent donc être approximée de la
sorte.
![]()



![]()
![]()
![]()

![]()
![]()
![]()
![]()

![]() . Ce
qui signifie que les niveaux dénergie accessibles aux électrons sont en deçà
du niveau de Fermi, par conséquent le gaz est totalement dégénéré et remplit
tous les niveaux jusquà e F.
. Ce
qui signifie que les niveaux dénergie accessibles aux électrons sont en deçà
du niveau de Fermi, par conséquent le gaz est totalement dégénéré et remplit
tous les niveaux jusquà e F.![]()
![]() = 0
ou 1.
= 0
ou 1.![]()

![]()


![]()

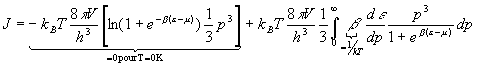
![]()



![]()
![]()
![]()
![]()
![]()




![]() :
:



![]()
















