Que s'est-il passé ?
 

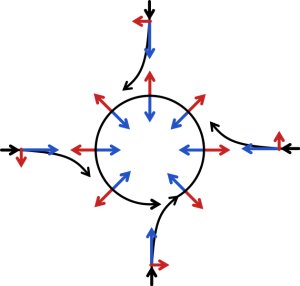
L'animation un peu plus bas donne effectivement un premier élément de réponse. Remarquez bien que pour cette animation, on se place dans l'espace, dans un référentiel dit absolu.

Comme on n'est plus sur terre, l'observateur flottant immobile dans l'espace voit donc bien la rotation de la terre pendant que l'obus vole en l'air après le tir. Un observateur sur terre, lui, est situé sur un référentiel dit « non galiléen » puisqu'il n'est pas en mouvement rectiligne uniforme (mais en rotation).

Les flèches violettes donnent la vitesse linéaire dite "tangentielle" pour le tank, l'obus et le bateau.

Il est  très important de comprendre que :

Si je reste toujours de mon point de vue d'un observateur dans l'espace, au moment du tir vers le Sud, le tank tire l'obus en l'air (l'obus va décrire un vol parabolique en raison de la gravité) et imprime du coup une composante de vitesse orienté SUD. Cependant, l'obus garde aussi la composante de vitesse linéaire tangentielle vers l'EST qu'il avait avec le tank avant son départ.

Que se passe-t-il durant tout le temps du vol de l'obus ?

Vous comprenez maintenant : l'obus va donc décrire sa parabole mais si le bateau est très loin et qu'il met du temps à parcourir sa trajectoire, il manquera sa cible car sa vitesse latérale n'est pas suffisante pour rattraper le navire sur un plan latéral.

Cela a l'air logique "sur le papier" mais je suis sur que vous vous dites :

Mais pourtant je visais au moment du tir dans le viseur.
Pire ! Durant tout le temps du vol, le navire est resté dans mon viseur ! ?
Ainsi, je regardais bien dans le viseur tout le temps que l'obus volait. Je n'ai rien corrigé.
J'ai bien vu par contre l'obus partir sur la droite et disparaître du navire.

Super Remarque-Question ! Cela m'amène au deuxième effet Coriolis. Car pour l'instant, on n'avait donné que la moitié de l'effet Coriolis : la différence de vitesses linéaire tangentielle entre le tank / obus et le navire; différence causée par la rotation et la forme de la terre .

La déviation que vous observez de votre tank n'est en fait pas seulement due à la différence de vitesse linéaire tangentielle en différents points du globe.
Cette déviation de l'obus va AUSSI dépendre du "changement d'orientation" (Les physiciens parlent eux de "conservation du moment angulaire"). Cela se traduit bien par le fait que vu de l'Espace, vous n'êtes plus en train de regarder dans la même direction entre le départ de l'obus et son arrivée.

Votre tank et le navire RESTENT SUR TERRE et s'orientent avec elle. L'obus, dans l'air lui, est « libre » de cette contrainte (l'air atmosphérique en rotation avec la terre pousse bien par frottement l'obus mais c'est négligeable). L'angle d'orientation de votre tank se modifie dans l'absolu et c'est la même chose pour le navire : vous restez tous deux dans un axe mobile.
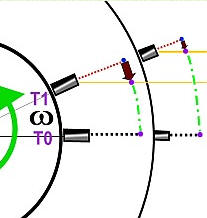
Sur l'illustration ci-contre, on a schématisé ce qui se passe : le tank est l'hexagone vert et le navire le triangle rose.

Le truc c'est de se rappeler que votre obus ne parcourt pas la distance de manière instantanée mais va mettre plusieurs minutes avant d'atteindre sa cible, devenue entre-temps « fantôme ». Il tombe bien là où vous vouliez mais c'est le bateau qui n'y est plus !

Vous avez peut-être envie de dire après tout cela : OK pour les tirs qui comportent une composante Nord-Sud. Quid des tirs Est-Ouest ?

On pourrait légitimement être tenter de penser :

Il n'y a pas de différence de vitesse tangentielle déjà puisqu'on est sur la même latitude !

C'est vrai, il reste à étudier le changement d'orientation que nous venons de voir dans le cas Nord-Sud. Afin de vous faire comprendre comment cet effet intervient, on préfère décomposer en 2 étapes de compréhension

Etape 1 : imaginons un canonnier et son canon posé sur la tranche d'un petit disque (on néglige la gravité).

Le canonnier possède une certaine vitesse tangentielle de translation due à la rotation du disque. Imaginons alors que l'obus qu'il va tirer ne va que deux fois plus vite que lui.

Vous voyez sur l'image ci-contre que dans ce cas, le canonnier tire son obus en ligne droite.

Seulement, au bout d'un certain angle de rotation, le canonnier qui regarde toujours dans la direction du canon, ne regarde plus dans la même direction que le vecteur vitesse de l'obus.

Si on se met à la place du canonnier (référentiel non galiléen), on aurait alors l'impression que l'obus effectue une parabole vers le haut, alors que vu de l'extérieur (référentiel galiléen), l'obus s'en va bien tout droit.

Attention ! Je vous vois déjà commencer conclure à tort : OK, donc Coriolis pour un tir Est-Ouest, c'est une déviation vers le haut ?

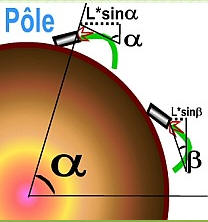
Etape 2 : Vous oubliez que l'exemple du disque n'est pas tout à fait représentatif de ce qui se passe sur Terre. La grosse différence, c'est que, sauf cas particulier de l'équateur, le canonnier ne se tient pas perpendiculairement au disque mais de biais puisque la gravité sur la Terre est orientée vers le centre.

Du coup, le référentiel de mesure du canonnier est "penché".

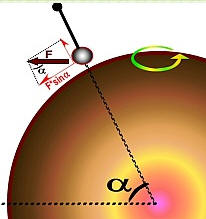
L'illustration ci-contre est une coupe de la Terre, du canonnier et de son canon : on remet la même déviation identifiée sur le modèle précédent du disque .

Le canonnier qui est maintenant "penché" va alors décomposer cette déviation en 2 composantes (en rouge). L'une qui pointe vers SON CIEL et l'autre parallèle à SON SOL, soit sa droite-gauche (en fait, le Sud et Nord respectivement si le canonnier tire vers l'Est).

La composante parallèle au sol est la déviation de Coriolis.

OK ! Et la déviation vers "le ciel du canonnier" ?

Et bien, c'est la seconde partie de l'effet Eötvos (au fait, pourquoi parle-t-on communément d'EFFET Eötvos et de FORCE de Coriolis : il faut choisir son camp !) que l'on a commencé à décrire dans l'article sur la force centrifuge.

Synthèse

Afin de compléter cet exemple de la fontaine de Coriolis, on va parler d'un exemple très simple de rotation

Il s'agit de la patineuse qui rapproche ses bras dans le but d'accroître sa vitesse de rotation. On a essayé d'illustrer la même chose avec une chaise pivotante et des haltères sur la vidéo. Pour simplifier, considérons que les bras de la patineuse sont infiniment légers mais qu'elle tient à bout de bras des haltères. Avec les modèles de physique classique, on parle de conservation du moment cinétique.

Peut-être ! En attendant, il est clair à présent que l'on peut aussi tout à fait parler d'effet de Coriolis pour expliquer cette augmentation de vitesse.

En effet, la patineuse —par l'effort de ses bras sur les haltères— contrecarre l'effet de Coriolis. Par conséquent, les haltères —de par et d'autres de l'axe (le corps de la patineuse)— par réaction (troisième loi de Newton) vont créer un couple sur les bras : ce couple va accroître ainsi la vitesse de rotation de la patineuse !

Or, pour les haltères ou pour la patineuse, ce n'est pas le cas : l'effort réalisé fait que les bras, qui sont rétractés vers le buste, restent dans l'axe initial tout au long de leur progression vers le buste.

Si cela se fait ainsi, c'est en réalité parce que la patineuse (ou moi avec les haltères) a agi pour les garder dans l'axe !

Il faut avouer qu'on ne se rend pas bien compte de cet effort particulier lorsqu'on réalise l'expérience mais il est nécessairement effectué sinon, les bras ne reviendraient pas en ligne droite mais dévierait d'autant plus fort qu'ils se rapprochent de l'axe central.

La vidéo ci-contre est similaire à celui plus classique de la patineuse : des personnes sur le bord extérieur d'un manège cherchent à se rendre au centre : la vitesse de rotation s'accroît fatalement lorsque l'on vise le centre.

Colonne de Taylor & Coriolis

C'est un peu technique et déborde (c'est le cas de le dire !) sur la mécanique des fluides mais c'est suffisamment intéressant pour le signaler.

Un "fan" de mécanique des fluides, Taylor, a eu l'idée de verser du colorant dans un liquide dont le récipient était en rotation (autour d'un axe central).

Le résultat est surprenant à première vue.

On constate que le colorant ne se diffuse pas horizontalement mais verticalement, dans une "colonne" du fluide.

En réalité, l'effet Coriolis est à l'oeuvre et lutte contre la diffusion horizontale du colorant qui doit suivre un chemin circulaire avec de très petits rayons.

Dans la vidéo ci-contre, on peut voir un récipient en rotation (la caméra tourne avec, c'est pour cela que la main de l'opérateur fait le tour ; en réalité, il est toujours au même endroit) et on engendre des remous turbulents avant de verser les colorants. Il y a deux caméras : celle du haut est en réalité une vue en coupe du récipient (afin de constater la diffusion verticale)

CyclonesLes grandes masses d'air obéissent bien à l'effet Coriolis.

Vous savez à quoi ressemble un cyclone : une masse de nuage qui s'enroule sur elle-même et avec la présence d'un "oeil" plutôt calme.

Pour comprendre ce qu''il se passe dans les cyclones, il faut généraliser d'abord avec la météorologie.

Soufflons un peu et parlons VENTS !

Comment le vent nait-il dans le ciel ?

REPONSE : à cause des différences de pressions (dues elles même à des différences de température) entre "coins du ciel".

Si vous avez quelques vagues notions, il existe des isobares (lignes courbes refermées et de même pression, comme le nom l'indique).
Une particule d'air a donc tendance à aller naturellement d'une isobare de haute pression vers une isobare de basse pression.

Or on sait maintenant que tout ce qui se meut sur et DANS l'HEMISPHERE NORD de notre Terre en rotation , va subir un effet de Coriolis qui dévie vers la DROITE du mouvement (lorsque l'observateur se déplace avec la Terre).

Une particule d'air donnée va donc aussi être déviée vers la droite (dans notre hémisphère nord) et cela jusqu'à ce que la force due à la différence de pression (qui initie le mouvement de cette particule d'air) et la force de Coriolis se retrouvent alignées, de même intensité mais de sens opposé : il y a équilibre des 2 forces.

C'est l' "équilibre géostrophique" dans le jargon des météorologue.

Cela signifie qu'une particule d'air identifiée va alors finir suivre un chemin parallèle aux isobares.

Le tout est donc de déterminer dans quel sens !
Cela dépend en réalité d'où se trouve l'isobare de haute pression et celle de basse pression : ou encore la particule a-t-elle suivi un mouvement centripète (vers l'intérieur) ou centrifuge (vers l'extérieur) ?

CONCLUSION : dans l'hémisphère nord (la photo ci-dessus est une masse dans l'hémisphère austral, juste pour voir si vous suivez), pour les masses d'air avec centres basse pression (les cyclones en particulier), le mouvement se fait contrairement aux aiguilles d'une montre.

Euuuh, attends-là, le sens inverse des aiguilles d'une montre, cela veut dire que la masse d'air est déviée vers la GAUCHE ! ? On disait que la particule d'air est déviée vers la DROITE ! Je ne comprends plus !

Le dessin ci-dessous (qui reste purement qualitatif : les flêches ne devraient pas être toutes aussi grandes en réalité) va vous éclairer sur ce qui se passe. Si la Terre ne tournait pas, la particule d'air irait tout droit vers le centre, là ou la pression est la plus faible.

Comme la Terre tourne, n'importe quel mouvement est affecté par l'effet Coriolis et dévie vers la droite par rapport à la trajectoire sans rotation de la Terre.

Il se produit donc un enroulement des masses d'air et le tout s'enroule vers dans le sens contraire des aiguilles d'une montre, donc vers la GAUCHE effectivement.

Faisons remarquer par contre que l'ensemble "cyclone" (tel n'importe quel objet) qui se déplace lui aussi dans l'atmosphère, va être dévié vers la DROITE.

Note : bien sûr, s'il on avait regardé une masse d'air à centre de haute pression dans l'hémisphère nord, cela aurait été l'inverse.

Je suis perplexe : on a dit que l'effet de Coriolis se révélait lorsque l'observateur était sur un référentiel en rotation …Mais alors, pourquoi VOIT-ON des cyclones se manifester depuis l'espace ?

Aaaah ! Excellente tentative d'objection !

En réalité, il ne faut pas oublier que le dessin ci-dessus n'est valable que dans le cas ou l'observateur tourne avec la Terre (un peu comme un satellite géostationnaire) : nous ne sommes pas dans un référentiel absolu de type galilléen dans le cas de ce dessin!.

OK, mais que devient ce schéma si on devient "un satellite non geostationnaire" mais "posé de manière absolue dans l'espace".

Si on veut sortir de ce schéma, il faut reprendre toute notre précédente analyse avec les boulets de canon ! (orientation Nord-Sud et Est-Ouest).

Si on s'amuse à décomposer la trajectoire des particules d'air avec nos précédentes histoires de boulets de canon et dans un référentiel externe et galiléen, on constate bien que ces particules d'air finissent bien par s'enrouler autour du centre de la dépression qui les attire (centre qui se déplace suivant une parallèle en accompagnant la rotation de la Terre) et qu'elles n'atteindront jamais.

Quand on aura le temps, on fera une animation afin de vous convaincre définitivement.

OK mais au fait, que se passe-t-il pour un cyclone à l'équateur ?

Comme l'effet de Coriolis est quasi-nul autour de l'équateur, une particule d'air attiré par une dépression locale situé au Nord ou au Sud d'elle peut s'y rendre "directos" : il n'y aura pas d'enroulement et un cyclone ne s'y formera jamais (pas de cyclone entre 5 ° sud et 5 ° nord).

Pour clore cette section sur les cyclones vous pouvez voir ci-contre une animation montrant que sur les autres planètes, les vents agissent de la même manière que sur Terre : d'où la magnifique tâche de Jupiter en rotation constante.

Le saviez-vous (1) ? : La rotation de la terre crée une force de Coriolis pour notre plus grand bénéfice. En effet, la déviation des courants d'air permet une meilleure distribution des masses d'air chaud et d'air froid. Si la terre ne tournait pas et donc si Coriolis n'existe pas, les masses d'air froides partiraient vers le sud directement, s'éleveraient en chauffant et il ne pleuvrait quasi-uniquement qu'à l'équateur.

Le saviez-vous (2) ? : Le sens de la rotation de la tâche de Jupiter est aussi dépendant de l'effet Coriolis

Le saviez-vous (3) ? : Tous les fluides en écoulement sont influencés par l'effet Coriolis. On aurait constaté que certaines berges de gauche ou de droite (selon l'hémisphère considéré) des lits de fleuves & rivières sont plus "usées" que l'autre en face, sur l'autre rive. Ainsi, on a cité dans l'article sur la force centrifuge les miroirs à bain de mercure. Et bien, il faudra les pencher afin qu'ils ne se déforment (astigmatisme) pas en raison de l'effet Coriolis dû à la rotation de la Terre.

Foucault

Ah! que d'émerveillement devant l'aspect magique de ce pendule qui oscille en changeant au fur et mesure du temps.

Demandez à la sortie d'un musée ce qu'ils ont compris de cette rotation et vous obtiendrez soit des explications loufoques (de la part des visiteurs) soit largement incomplètes (de la part des guides), soit des équations (de la part des chercheurs-ingénieurs).

Bon, d'un autre côté, on ne peut pas trop leur en vouloir car jusqu'au début du siècle dernier on débatait encore du fait que ce pendule modifie son plan d'orientation et surtout que le temps qu'il met à faire un tour complet dans notre référentiel terrestre dépend de la latitude.

Vous allez pouvoir mieux comprendre si vous avez lu tout ce qui précède sur le tir d'un obus grâce à quelques schémas supplémentaires.

En effet, un pendule peut être plus ou moins considéré comme un obus qui ferait des aller-retour en l'air. Les différences avec l'exemple de l'obus sont :

Léon Foucault est un homme admirable : non pas un chercheur classique mais plutôt un petit Einstein sorti du Néant par son intellect lui aussi.

Il va être inspiré par l'observation fortuite d'un mouvement "gyroscopique" (il inventera le gyroscope plus tard) du mandrin d'un tour en rotation.

Il va avoir cette idée géniale du pendule et va l'expérimenter dans sa cave.

Pas très précis au départ mais il va éliminer le maximum de perturbations et un jour ça marche !

Il a compris que l'orientation du plan d'oscillation du pendule va fatalement se modifier en raison de la rotation de la Terre. Il n'avait cependant a priori pas tout compris quant-aux variations dans le temps mis par le pendule à tourner.

POUR COMPRENDRE EN 2 SECS LA BASE DU FONCTIONNEMENT DU PENDULE DE FOUCAULT

En fait, la base du raisonnement de Foucault est très aisément compréhensible et calculable lorsqu'on se place aux poles (Nord ou Sud).

En effet, dans ce cas, l'axe de rotation de la Terre passe pile poile dans le plan d'oscillation du pendule et l'axe de rotation de la Terre passe toujours par le point d'accroche du pendule quelque soit l'angle de son plan d'orientation.

Du coup, il est aisé de comprendre que, vu d'un reférentiel "absolu", pendant qu'un explorateur qui se tient immobile au pole va tourner sur lui-même en 24h00 (grosso-modo), le pendule, lui, va rester fixe par rapport à ce repère absolu. DONC, du point de vue de l'observateur, c'est le plan d'oscillation du pendule qui va tourner sur lui-même en 24h00.
Pour l'anecdote, des chercheurs ont d'ailleurs en avoir le coeur net : la vérification au Pole-Sud (anglais).

On peut d'ailleurs constater cela grâce à cette vidéo d'une expérience astucieuse à échelle réduite pour observer la rotation du pendule aux poles.

La même expérience permet de constater que le plan du pendule ne tourne pas à l'équateur (vidéo).

Revenons à Léon de Foucault.

Fort de son test, Foucault fait une petite expo dans le Panthéon à Paris où il a suspendu le pendule et invité plein de témoins.

Vous êtes invité à venir voir tourner la Terre, demain de trois à cinq heures

Il y avait bien eu la conviction et quelques expériences peu fiables de déviation de chute des corps par Galilée puis des preuves indirectes (à partir de données astronomiques reposant sur des spéculations théoriques) mais là, la preuve est directe, fiable et indiscutable : rien d'autre ne peut expliquer cette déviation répétée et calculable.

Pour l'explication, vous nous voyez venir gros comme un camion : on encore voir deux types de pendules. D'abord celui qui oscillerait dans un plan Nord-Sud puis un autre dans le plan Est-Ouest. Tous les autres se déduieront par combinaison des deux mouvements.

 

ORIENTATION NORD-SUD DU PENDULE 

Le pendule, peut être étudié comme un obus (qui ferait des aller-retours du canon vers la cible) hormis qu'il n'y a pas de différence de vitesse de translation

(Enfin, il y a eu une si on veut être super tatillon car la vitesse de translation n'est pas exactement la même entre le l'endroit du lâcher et celui de l'apogée de l'autre côté mais cela reste extrêmement faible en raison de la distance parcourue ; le pendule ne va pas tout droit mais va très très très légèrement osciller latéralement en raison de la tension "correctrice" du cable.
Arrêtons de couper les cheveux en 4 là …).

 

Donc, il reste le fait que l'angle d'orientation de la pièce va changer au cours du temps (ainsi que la verticalité du plan du pendule à cause de l'action de la gravité).

On suppose en effet que le pendule est suspendu dans une pièce carrée : il y a donc un mur Nord et un mur Sud.

La droite Nord-Sud, perpendiculaire aux 2 murs va changer d'orientation avec la rotation de la Terre, comme le faisait la droite qui joignait le tank au navire dans l'exemple précédent.

On remarque que l'angle de cette droite Nord-Sud par rapport à un référentiel absolu dans l'espace va tourner en 24 heures au pôles et jamais (temps infini) à l'équateur (toujours orienté "vers le bas") : dans les 2 cas, la direction verticale du plan du pendule reste fixe par rapport aux étoiles lointaines et garde la direction latérale au pôle seulement.

Entre le pôle et l'équateur, on sent intuitivement qu'on va passer de 24 h à l'infini selon la latitude : à la latitude de Paris par exemple, un observateur voit le pendule faire un tour complet en 32 heures.

Ce fait (pourquoi 32 heures ?) a interloqué beaucoup de scientifiques éminents !

Afin de mieux comprendre ce qui se passe entre les 2 situations simples : pôles (T=24 h) et équateur (T= infini) , on va réaliser des modèles avec des canons qui seront placés en deux endroits différents du globe : l'un plutôt proche du pôle et l'autre de l'équateur.

Ensuite, on va comparer ce qui se passe à partir de 2 points de vue : l'un vu du dessus du pôle et l'autre de la Terre en coupe. On va alors appliquer le même effet Coriolis (le revoilà !)

Sur la première image, on voit la Terre en coupe et les 2 canons tirer : ce que l'on remarque instantanément, c'est qu'il s'agit de la même trajectoire parabolique sauf qu'elle n'est pas orientée de la même manière vue de d'un référentiel absolu dans l'espace.

On note que si on projette la distance que fait la parabole du tir sur l'axe des abscisses X , cette projection est bien plus importante pour le canon près du pôle que celui près de l'équateur.

On peut calculer que la longueur p de cette projection =

p = distance L * sinα

où L est la distance parcourue par l'obus.

On fait de même avec l'autre canon et la projection est plus faible car :

β < α .

Voyons à présent ce qui se passe avec une vue du dessus : dans ce cas, on se rapproche de la configuration d'un disque tournant.

On voit à T0 les 2 canons tirer : mais ce que l'on voit avec cette vue, c'est la projection sur l'axe des abscisses de la distance que parcoure l'obus. A T1, les deux obus ont terminé leur trajectoire parabolique (en frappant le sol) et la terre a tourné dans l'intervalle du vol des obus.

Les canonniers observent à T1 des déviations par rapport à la trajectoire qu'il présume dans son référentiel tournant (ce serait la trajectoire du tir d'un nouvel obus à T1) : l'importance de cette déviation constatée par le canonnier (qui regarde toujours dans l'axe de son canon) est manifestement proportionnelle à la distance projetée sur l'axe des abscisses X (passant par l'équateur) de la parabole de l'obus.

Cette déviation observée par le canonnier (dans son référentiel tournant) est orientée vers la droite de ce dernier (on est depuis le début dans l'hémisphère Nord ).

Conclusion sur le mouvement Nord-Sud du pendule

Le canonnier observe une déviation vers la droite qui est proportionelle à sin α

 ORIENTATION EST-OUEST DU PENDULE 

Lors du lâché du pendule soulevé à l'Ouest et lancé initialement vers l'Est, on se retrouve dans la même configuration que celle du tir du tank vers l'Est un peu avant.

Le canonnier voit donc à la fois une déviation vers la droite (remarque : quand le pendule fait le chemin inverse, la force s'inverse mais reste sur la droite de la trajectoire donc tout se tient) et vers son ciel.

On précise avec le dessin ci-contre que l'intensité de la déviation dépend du sinα : angle que fait le pendule avec l'axe des abscisses.

Remarquez à nouveau au passage qu'il y a cette fois une partie de l'effet Eötvos qui se manifeste (sauf au pôle).

Seulement, ce sera le contraire quand la boule du pendule fera le chemin inverse (Ouest›Est) : le pendule ne perd donc pas son énergie initiale mais il remonte plus haut du côté Est (sauf au pôle encore une fois).

Cet partie de l'effet Eötvos est bien sur maximal à l'équateur.

Voilà : le plan d'un pendule quelconque est un mélange d'orientation Est-Ouest et Nord-Sud. Vous détenez toute l'explication sur le fonctionnement du pendule de Foucault. On espère que les explications et dessins étaient suffisamment clairs.