Johannes KEPLER

Ses trois lois sur les orbites des planètes sont l'acquis empirique le plus important de l'histoire de l'astronomie.

Johannes Kepler est né près de Weil, dans le Wurtemberg, le 27 décembre 1571. Issu d'une famille pauvre et d'une constitution fragile, il fréquenta cependant l'université de Tübingen grâce à une bourse octroyée par le duc de Wurtemberg. A vingt ans, il obtint le diplôme de magister artium, selon lui “un heureux accident de parcours” qui lui permit de ne pas devoir poursuivre des études de théologie. En effet, il alla aussitôt occuper à Graz, en Styrie, le poste laissé vacant par le professeur de mathématiques du duché. On lui avait assigné la compilation du calendrier annuel qui, à la différence de ceux d'aujourd'hui, devait prévoir aussi bien les aléas météorologiques que les péripéties politiques importantes de l'année à venir. Dans son premier numéro, en 1595, il prévit justement un hiver rude et l'invasion des Turcs, ce qui assit définitivement sa réputation.

Alors, il travaillait aussi à son premier grand ouvrage, fondé sur deux piliers fondamentaux : la géométrie euclidienne et la théorie de Copernic, publiée cinquante années auparavant.

Le successeur de Brahe

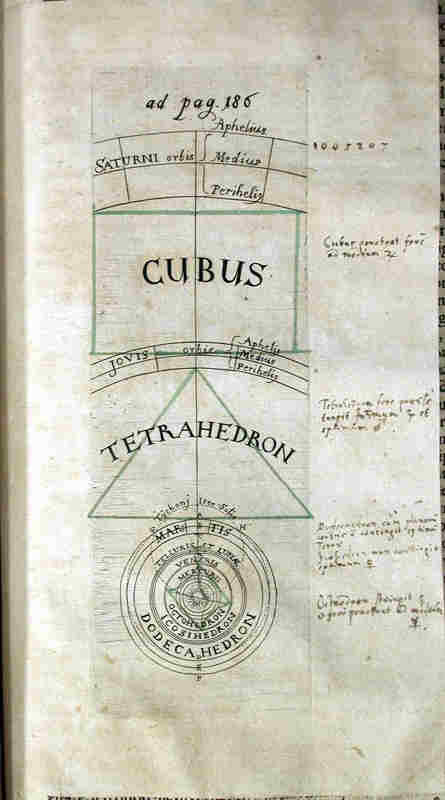
Il s'agissait du Mysterium Cosmographicum, une oeuvre de jeunesse très importante, car elle contient déjà le principe qui inspirera les ouvrages suivants. Kepler pensait qu'il y avait correspondance entre les orbites des six planètes connues et les cinq solides réguliers euclidiens, ceux dont les côté forment des polygones réguliers. Selon lui, ces solides devaient se trouver à la place des anciennes “sphères”, entre les orbites des planètes : l'hypothèse supposait que les sommets du solide touchaient l'orbite de la planète la plus extérieure pendant que l'orbite de la planète immédiatement à l'intérieur était tangente aux centres de leurs côtés. Cette géométrie néoplatonicienne fut interprétée par beaucoup comme une pure spéculation, mais elle permit en fait à Kepler d'énoncer sa “troisième loi”, et d'établir ainsi les proportions et les distances à l'intérieur du système planétaire.

L'astronome Tycho Brahe considéra le Mysterium comme l'oeuvre d'un génie et prit Kepler pour assistant à Prague, dans l'espoir qu'il l'aiderait à résoudre le problème de Mars, dont l'orbite ne correspondait pas à l'ensemble des observations faites à Uraniborg, données dix fois plus précises que celles recueillies jusque-là.

Kepler succéda à son maître danois à la mort de ce dernier, en 1601, comme astronome impérial et entreprit aussitôt de traiter ces données. C'est ainsi qu'il découvrit l'existence de la réfraction atmosphérique et qu'il inventa (en approfondissant ses études d'optique) l'oculaire à lentille biconvexe (ou dioptrice, 1611) toujours en usage.

En 1602, il découvrit sa “seconde loi” sur les aires égales balayées en des temps égaux par les rayons vecteurs des planètes (qui relient Soleil et planètes) et, quelques années après, celle des trajectoires elliptiques des mouvements orbitaux. Il publia ces résultats dans son Astronomia Nova, ainsi que son hypothèse révolutionnaire selon laquelle les mouvements des planètes étaient dus à une action du Soleil, action moins importante quand la planète est plus éloignée. Il introduisit en outre une nomenclature moderne avec des termes tels que foyer de l'ellipse, satellite, intertie. En 1604, il observa une “nova” dont on peut encore aujourd'hui observer les restes nébuleux.

Harmonies célestes et guerres de religion

En 1612, Kepler alla s'installer à Linz et n'arrêta alors plus de rebondir dans une Europe déchirée par les guerres de religion. Dans l'ouvrage le plus important de la deuxième partie de sa vie, Harmonices Mundi (1619), il chercha des correspondances harmoniques entre les vitesses planétaires : il y affirma que les rapports entre les vitesses maximale et minimale sont exprimés par des nombres entiers, comme en musique. En 1627, il publia les Tabulae Rudolphinae, tâche que Brahe lui avait confié vingt-cinq ans auparavant.

Il mourut en 1630 à Ratisbonne, sans que la portée immense de son oeuvre fût reconnue, ni par Galilée ni par Descartes. Mais bientôt Newton viendrait, qui prendra ses travaux comme point de départ des siens.