Les indicateurs de distance

Il s’agit de classes homogènes d’objets servant à déterminer, par comparaison, la distance des galaxies les plus lointaines.

La connaissance des propriétés des corps célestes dépend d’une manière critique de nos capacités à mesurer les distances D : il suffit de penser, par exemple, que la valeur absolue des luminosités est proportionnelle à D².

Le terme indicateur de distance concerne cet ensemble d’objets ou phénomènes célestes grâce auxquels les astronomes s’ingénient à combler l’immense lacune existant entre les domaines d’application des seules deux méthodes directes pour mesurer les distances astronomiques :

• Les parallaxes trigonométriques : les parallaxes annuelles p" (en secondes d’arc) donnent des mesures de distance D = 1/p" fiables tout au plus jusqu’à quelques centaines d’années-lumière, même si l’on a recours aux techniques d’observation sophistiquées faites depuis l’espace ; ces mesures se fondent sur la détermination exacte du rayon moyen de l’orbite terrestre, l’unité astronomique (1 pc = 206.265 u.a)
  
• La loi de Hubble : si on établit une proportionnalité directe entre distance et vitesse de récession cosmologique (à travers le redshift z), ie. si l’on utilise la loi de Hubble, c’est pour des distances inférieures à 50 millions de parsecs – au-dessous de cette limite, les vitesses des galaxies et celle de l’observateur ne sont plus négligeables mais elles dépendent de toute façon d’un paramètre qu’il n’a toujours pas été possible de déterminer précisément à ce jour, la constante de Hubble H_o. En effet, la distance D est donnée par la formule

Pour déterminer les distances entre 10 parsecs et 50 millions de parsecs, et obtenir H_o en associant ce paramètre à l’unité de mesure de base, on a d’abord recours aux indicateurs photométriques. Il s’agit de familles d’objets homogènes dont la luminosité observée (donc apparente) est rapportée à ce qu’elle serait s’ils étaient situés à la distance standard de 10 parsecs. Cette luminosité absolue L s’obtient en étalonnant la famille en question à l’aide d’un ou plusieurs indicateurs à rayon plus court, étalonnés à leur tour selon une chaîne qui se déroule vers le bas, jusqu’à ce qu’on entre dans la sphère d’action des parallaxes trigonométriques.

Toute la pyramide des indicateurs repose sur les bases fragiles d’une méthodologie imposant un étalonnage à la chaîne – avec répercussion des imprécisions de chaque indicateur sur tous ceux qui dépendent de lui – et se fonde sur le postulat hardi et dont on abuse souvent de l’homogénéité de la Nature, attribué à Hubble mais implicite dan le travail de l’astronome.

Par ailleurs, les indicateurs photométriques sont affectés indistinctement d’une erreur systématique, appelées préjugé de Malmquist, due à la sélection de l’échantillon d’observation : en fixant, comme c’est l’usage, une limite à la luminosité apparente des objets d’une famille, on discrimine par force les objets intrinsèquement plus faibles. Les valeurs moyennes sont ainsi faussées et il en résulte des distances fictivement grandes. C’est ce qui se passe pour l’échantillon des étoiles visibles à l’œil nu sur la voûte céleste : celles qui sont intrinsèquement plus faibles sont des astres proches de nous, alors que les étoiles intrinsèquement lumineuses peuvent être très lointaines.

Ces incertitudes associées à d’autres sont à l’origine de l’éternel débat sur les distances des galaxies proches et, en dernière instance, sur la valeur de la constante de Hubble (et ainsi sur l’âge de l’Univers).

Parmi les principaux indicateurs photométriques, il faut signaler certaines catégories d’étoiles variables, régulières ou chaotiques : les RR Lyrae, les céphéides, les novae et les supernovae.

Les RR Lyrae sont des étoiles évoluées, sujettes à une phase d’instabilité ; c’est pourquoi leur luminosité varie rapidement en achevant une oscillation complète en moins d’un jour. En revanche, leur luminosité moyenne est constante (environ 50 fois celle du Soleil). Ces « chandelles-standard » sont bien caractérisées par leur courbe de lumière, qui les distingue nettement des autres types d’étoiles variables et que l’on peut découvrir et observer, grâce aux technologies actuelles, jusqu’aux confins du Groupe Local (environ 1,5 million de parsecs).

Les Céphéides sont aussi des variables régulières. Il s’agit d’étoiles puissantes jeunes, qui ont cependant des sosies parmi les étoiles évoluées du type W Virginis, six fois plus faibles que les Céphéides mais à période égales, ce qui démontre au passage que la nature n’est pas toujours homogène (!). Il y a 90 ans, en étudiant la population des étoiles variables dans les Nuages de Magellan, l’astronome américaine Henrietta Leavitt découvrit que la luminosité moyenne des Céphéides augmente proportionnellement au logarithme de la période P de la pulsation lumineuse : les Céphéides de période P = 5 jours sont environ trois fois plus lumineuses que les RR Lyrae et trois cents fois plus brillantes que celles de période P = 50 jours. La couleur varie aussi quand P augmente, en passant du rouge au bleu. Actuellement, le rapport entre période et luminosité a été étalonné sur les Céphéides des amas ouverts de la Voie Lactée et les variables des galaxies proches. Il y a de nombreuses Céphéides utilisables, jusqu’à 5 millions de parsecs, et maintenant encore davantage avec les perspectives qu’a ouvertes le télescope spatial Hubble. Faciles à localiser, elles présentent néanmoins les inconvénients propres aux populations d’étoiles jeunes, en particulier l’association avec des poussières provoquant des absorptions qui nous font sous-évaluer leur luminosité apparente ; par ailleurs, leur éclat dépend de la composition chimique, qui varie considérablement d’une galaxie à l’autre.

Fig. 2 Diagramme période-luminosité pour les Céphéides du Grand Nuage de Magellan et celles de la galaxie NGC 3109 dans le domaine de la lumière bleue et dans le visible. Les variables du Grand Nuage ont été enregistrées comme si elles étaient 800 fois plus faibles qu’elles ne le sont pour compenser la grande proximité de cette galaxie par rapport au Soleil.

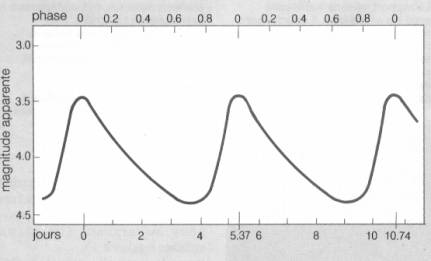
Fig. 3 Courbe de lumière de delta Cephei, le prototype des Céphéides. Sa variation de luminosité – 2,2 fois plus lumineuse au maximum – se reproduit avec une précision chronologique tous les 5,336 jours, soit 5 jours 8 heures et 47 minutes.

Les novae sont des variables explosives qui, à leur luminosité maximale, peuvent atteindre la splendeur de presque un million de Soleils ; on peut ainsi les observer jusqu’à 20 millions de parsecs. La rapidité avec laquelle la luminosité décline après le maximum permet de mesurer les distances avec une marge d’erreur de 20%. La relation a été établie à partir de novae observées dans la galaxie d’Andromède (M31) dans laquelle éclatent en moyenne 30 novae par an.

Fig. 5 Deux novae découvertes dans les régions centrales de la proche galaxie d’Andromède (objet Messier 31)

Les supernovae du type Ia sont une classe de variables catastrophiques, communes à tous les types de galaxies, avec courbes de lumière et spectres qui se répètent d’un cas à l’autre. D’après les observations, les modèles théoriques suggèrent que la luminosité maximale est dix milliards de fois supérieure à celle du Soleil, et constante à 25% près. Ces supernovae sont utilisables jusqu’à une distance d’un milliard de parsecs.

Fig. 6 Image de la supernova 1992C, apparue dans la galaxie NGC 3367, une spirale barrée à 200 millions d’années-lumière de nous. Sur cette photo, prise 20 jours après le maximum de la courbe de luminosité, la supernova (en bas du cliché) est encore intrinsèquement un milliard de fois plus brillante que le Soleil…

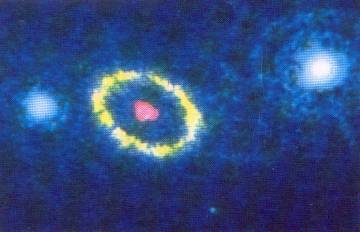
Fig. 7 Image de la supernova 1987A apparue dans le Grand Nuage de Magellan, à 170.000 années-lumière de nous. La photo, prise dans la raie verte de l’oxygène ionisé deux fois avec la Faint Object Camera du HST et colorée artificiellement à l’ordinateur, montre la structure complexe des estes de l’étoile explosée (tache rougeâtre au centre). L’anneau qui les entoure (en jaune) existait avant l’explosion : il s’agit du matériau éjecté par l’étoile génitrice avant l’explosion catastrophique et destiné a à être balayé par l’onde de choc en l’espace d’une seconde.

Enfin, il faut noter ici les résultats très précis sur la position de 120.000 étoiles obtenus par la télescope astrométrique de l’ESA, emmené par Hipparcos, qui vont permettre un meilleur calibrage de centaines de chandelles-standard.

En effet, d’autres méthodes sont envisageables pour déterminer la distance des étoiles.

• A partir de l’étude comparée des spectres de milliers d’étoiles, on peut repérer des caractéristiques distinctives de leur luminosité. A titre d’exemple, les étoiles très lumineuses (géantes et supergéantes) ont des raies spectrales minces alors que celles des étoiles faibles sont larges. Patiemment, on a défini des critères permettant d’établir la magnitude absolue, et donc la distance d’une étoile à partir de l’examen de ses raies spectrales.
• Il existe une méthode dite dynamique qui a recours aux étoiles doubles. On sait qu’entre période de révolution P (en années), distance totale a (en u.a) entre les étoiles et masse totale M (en masses solaires) il existe le rapport dynamique

Ce rapport a été utilisé essentiellement pour trouver la masse des étoiles, mais par la suite on a pu en faire un usage inverse : trouver a en fonction de la masse. Par ailleurs, les observations fournissent la valeur angulaire de a (a" en secondes d’arc) et la simple formule

donne la distance en parsecs du couple par rapport à nous. On trouve ainsi la masse directement, sans passer par la parallaxe trigonométrique ; on a coutume d’appeler ce procédé la « méthode des parallaxes dynamiques ». Pour connaître la masse du couple, on est aidé par le fait qu’à la différence des luminosités, variant avec des écarts énormes, les masses des étoiles ont des variations contenues : pour une très grande majorité des étoiles observables, elles sont comprises entre 0,3 et 3 fois la masse solaire. Ainsi, si l’on attribue à chaque étoile du couple la masse 1, la distance trouvée a une marge d’erreur de 40%, et pas plus.

A partir de la distance d obtenue ainsi, on déduit les magnitudes absolues des deux étoiles et avec celles-ci, grâce au rapport masse-luminosité, on peut dans bien des cas obtenir des valeurs de masses plus proches de la vérité que celles supposées auparavant. Avec cette nouvelle valeur de M, on applique à nouvelle la formule de la parallaxe dynamique pour avoir une valeur plus précise de a et donc de la distance d.