
Le pentagone
On se pose la question : comment faire pour tracer un pentagone ? On peut prendre un rapporteur et séparer un cercle en cinq secteurs de 72° chacun... mais il existe des méthodes géométriques un peu plus évoluées...
Tracer un cercle (c1) de centre O, passant par A. On choisira comme unité le rayon du cercle. Placer un diamètre [AA'] et [OB'] un rayon perpendiculaire à [AA'].
K est le milieu de [OA'], le cercle (c2) de centre K et de rayon KB' coupe [OA] en U. La longueur du côté du pentagone est égal à B'U.
La médiatrice de [OU] coupe le premier cercle (c1) aux points B et E qui sont deux sommets du pentagone. Le cercle de centre B passant par A recoupe (c1) en C. Le symétrique D de C par rapport à (AA') termine la construction du pentagone.

En effet KB' = KU =
![]() d'après la propriété de Pythagore dans le triangle OKB' rectangle en O, donc OU
=
d'après la propriété de Pythagore dans le triangle OKB' rectangle en O, donc OU
=
![]() -
-
![]() =
=
![]() et OI =
et OI = 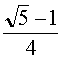 .
L'angle (
.
L'angle (![]() ,
,
![]() )
a un cosinus égal à
)
a un cosinus égal à
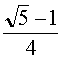 ,
c'est bien un angle de
,
c'est bien un angle de
![]() .
La corde [AB] est donc le premier côté du pentagone régulier convexe ABCDE. [EB]
est un côté du pentagone étoilé EBDAC contenu dans le même cercle.
.
La corde [AB] est donc le premier côté du pentagone régulier convexe ABCDE. [EB]
est un côté du pentagone étoilé EBDAC contenu dans le même cercle.
Placer les points O et A, tracer le cercle (c1) de centre O passant par A, placer le symétrique A' de A par rapport à O.
Sur un rayon perpendiculaire au diamètre [AA'], placer le point K au milieu de ce rayon.
Tracer le cercle (c2) de centre K passant par A, ce cercle coupe la droite (OK) en U et T. AU est égal à la longueur du côté d'un pentagone convexe inscrit dans le cercle (c1), AT est égal à la longueur du pentagone croisé.
Tracer les cercles (c3) et (c4) de centre A, passant par U et T. Le cercle (c3) coupe (c1) en B et E. Le cercle (c4) coupe (c1) en C et D.

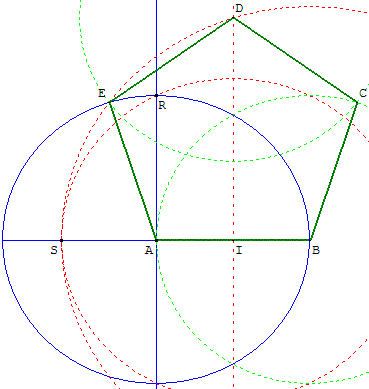
Tracer un cercle (c1) de centre O, passant par A. Placer un diamètre [AA'] et [OB'] un rayon perpendiculaire à [AA'].
P est au quart de [OA'] à partir de O : OP =
![]() OA' et Q est le milieu de [OB'], le cercle (c3) de centre P et
passant par Q coupe [OA] en I et [OA'] en J. La perpendiculaire en I à (AA')
coupe le cercle (c1) en B et E. La perpendiculaire en J à
(AA') coupe le cercle (c1) en C et D (placés suivant la
figure).
OA' et Q est le milieu de [OB'], le cercle (c3) de centre P et
passant par Q coupe [OA] en I et [OA'] en J. La perpendiculaire en I à (AA')
coupe le cercle (c1) en B et E. La perpendiculaire en J à
(AA') coupe le cercle (c1) en C et D (placés suivant la
figure).
ABCDE est un pentagone régulier.

Démonstration à l'aide du produit scalaire (1ère S)
pour le prouver il suffit démontrer que AÔB =
![]() et AÔC =
et AÔC =
![]() .
.
On choisira comme unité le rayon du cercle.
Dans le triangle rectangle OPQ le théorème de Pythagore permet de trouver :
PQ =
![]() et OI = PI - PO = PQ -
et OI = PI - PO = PQ -
![]() =
=
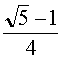 .
.
I étant la projection orthogonale de B sur (OA), on trouve l'égalité des produits scalaires :
|
|
=
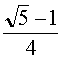 . . |
Ce produit scalaire s'exprime en fonction de l'angle des vecteurs :
|
|
=
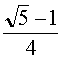 , , |
donc cos(AÔB) =
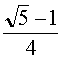 ;
AÔB =
;
AÔB =
![]() .
.
De même OJ = OP + PJ =
![]() + PQ =
+ PQ =
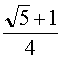 .
.
J étant la projection orthogonale de C sur (OA), on a :
|
|
=
 , , |
et en fonction de l'angle des vecteurs :
|
|
=
 , , |
donc cos(AÔC) =
 ;
la formule de duplication cos(2x) = 2cos2x - 1 permet,
en vérifiant que 2cos2
;
la formule de duplication cos(2x) = 2cos2x - 1 permet,
en vérifiant que 2cos2
![]() - 1 =
- 1 =
 ,
de déduire que AÔC =
,
de déduire que AÔC =
![]() .
.
Les points D et E étant les symétriques de C et B par rapport à (OA), on a
donc AÔD =
![]() et AÔE =
et AÔE =
![]() ,
la figure est bien un pentagone régulier.
,
la figure est bien un pentagone régulier.
Démonstration utilisant les nombres complexes (Teminale S) :
dans le plan complexe choisira comme origine le centre du pentagone et pour A le point d'affixe 1.
Pour le prouver il suffit démontrer que les sommets sont les racines
cinquième de l'unité :
1, z =
![]() ,
z2,
,
z2,
![]() ,
,
![]() ;
solutions de l'équation z5 - 1 = 0.
;
solutions de l'équation z5 - 1 = 0.
Le polynôme z5 - 1 se factorise sous la forme z5 - 1 = (z - 1)( z4 + z3 + z2 + z + 1) (formule classique de la somme des 5 premiers termes d'une suite géométrique).
La factorisation peut se poursuivre par z5 - 1 = (z
- 1) (z2 - 2αz + 1) (z2 - 2βz
+ 1) avec, par identification, les réels α et β vérifiant :
a + b = -
![]() et
ab = -
et
ab = -
![]() .
.
Dans le triangle IJQ rectangle en Q, P est le milieu de [IJ] donc OI - OJ =
-2 OP = -
![]() ;
;
la relation métrique pour la hauteur [OQ] permet d'écrire :
OI × OJ = OQ2 =
![]() .
α et β sont donc les affixes des points I et J.
.
α et β sont donc les affixes des points I et J.
Il est possible de résoudre le système d'équations α + β = -
![]() et
α β = -
et
α β = -
![]() et les réels α et β sont les solutions d'une équation du second degré, mais
utilisons plutôt la calculatrice TI-92 qui permet de factoriser dans C et
en regroupant les facteurs trouvés avec factorC(z^5- 1,z) on a :
et les réels α et β sont les solutions d'une équation du second degré, mais
utilisons plutôt la calculatrice TI-92 qui permet de factoriser dans C et
en regroupant les facteurs trouvés avec factorC(z^5- 1,z) on a :
(z2 - 2αz + 1) =

et (z2 - 2βz + 1) =
 ,
,
soit z5 - 1 = (z - 1) .
.
Dans tous les cas (en vérifiant éventuellement les valeurs des cosinus) on trouve :
α =
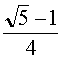 =
Re(
=
Re(![]() ) ;
partie réelle des solutions de z2 - 2αz + 1 = 0,
) ;
partie réelle des solutions de z2 - 2αz + 1 = 0,
et β =
 =
Re(
=
Re(![]() ) ;
partie réelle des solutions de z2 - 2βz + 1 = 0.
) ;
partie réelle des solutions de z2 - 2βz + 1 = 0.
α et β sont les parties réelles des racines cinquièmes de l'unité imaginaires. Les sommets du pentagone régulier sont bien l'intersection du cercle unité avec les parallèles à (Oy) passant par I et J.
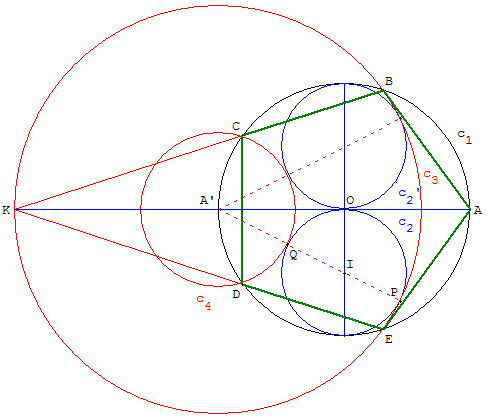
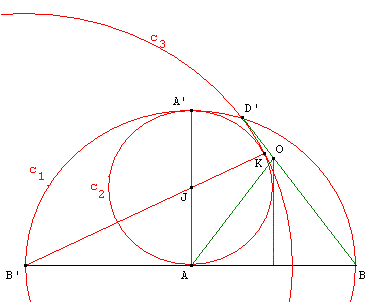
Construction de Dumont (cercles tangents)
Construction proposée par Dumont (1996) à propos des tracés régulateurs des temples d'Angkor.
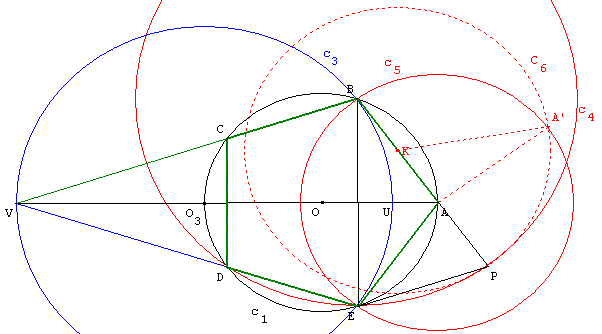
Placer deux points O, A et le cercle (c1) de centre O, de
rayon r, passant par A. A' est le symétrique de A par rapport à O. I est
le milieu d'un rayon perpendiculaire au diamètre [AA']. (c2)
est le cercle de centre I et de rayon
![]() .
La droite (A'I) coupe le cercle (c2) en P et Q. (c3)
et (c4) sont les cercles de centre A' tangents à (c2).
Le cercle (c3) est tangent intérieurement au cercle (c2)
en P et le cercle (c4) est tangent extérieurement au cercle (c2)
en Q. Le cercle (c3) coupe (c1) en B et E et
le cercle (c4) coupe (c1) en C et D. Les
points ABCDE sont les sommets du pentagone cherché.
.
La droite (A'I) coupe le cercle (c2) en P et Q. (c3)
et (c4) sont les cercles de centre A' tangents à (c2).
Le cercle (c3) est tangent intérieurement au cercle (c2)
en P et le cercle (c4) est tangent extérieurement au cercle (c2)
en Q. Le cercle (c3) coupe (c1) en B et E et
le cercle (c4) coupe (c1) en C et D. Les
points ABCDE sont les sommets du pentagone cherché.
Démonstration
Dans triangle rectangle A'OI on a (puissance du point A' par rapport au cercle c2) :
A'O2 = A'I2 - IO2 = A'I2 -
![]()
A'O2 = (A'I -
![]() )(A'I
+
)(A'I
+
![]() )
)
A'O2 = (A'I - IQ)(A'I +IP) = A'Q . A'P.
A'O2 est donc le produit des rayons des cercles (c3) et (c4).
Soit M le point d'intersection du segment [A'B] et du cercle (c4).
Le produit des rayons est donc :
A'O2 = A'M . A'B, soit
![]() .
.
Ayant déjà l'angle OÂ'B en commun les triangles A'MO et A'OB sont semblables.
Le triangle A'OB ayant deux côtés égaux à r est isocèle, le triangle A'MO l'est aussi.
Soit α la mesure des angles égaux OÂ'B =
![]() = MÔA'.
= MÔA'.
Les angles « au sommet » des triangles isocèles sont donc
![]() = A'ÔB = π - 2α.
= A'ÔB = π - 2α.
D'autre part, le triangle BOM est isocèle (puisque BM = r). D'où MÔB =
![]() .
.
On a donc A'ÔB = π - 2α = A'ÔM + MÔB= α +
![]() .
.
De là α =
![]() ,
MÔB =
,
MÔB =
![]() ,
A'ÔB =
,
A'ÔB =
![]() .
Donc AÔB =
.
Donc AÔB =
![]() et B est le deuxième sommet du pentagone.
et B est le deuxième sommet du pentagone.
Le point C d'intersection de la demi-droite [OM) et du cercle (c1)
est le troisième sommet du pentagone car : CÔB = MÔB =
![]() .
Montrons que ce sommet C du pentagone est sur le cercle (c4).
.
Montrons que ce sommet C du pentagone est sur le cercle (c4).
L'angle CÂ'B inscrit dans le cercle (c1) est égal à la
moitié de l'angle au centre : CÂ'B =
![]() CÔB =
CÔB =
![]() .
.
![]() = MÔB =
= MÔB =
![]() .
.
Le troisième angle du triangle A'MC est
![]() =
=
![]() .
Ce triangle ayant deux angles égaux est isocèle. A'M = A'C. C est bien sur le
cercle (c4).
.
Ce triangle ayant deux angles égaux est isocèle. A'M = A'C. C est bien sur le
cercle (c4).
La symétrie par rapport à (AA') donne les autres sommets E et D.
Cette figure est la représentation de l'il
d'Oudjat vue par les égyptiens.
Les deux arcs de cercle RS forment ce que les mathématiciens appellent
une lentille.

Les points B et E, intersection du cercle de diamètre [AO'] et d'un des arcs RS, sont deux des sommets du pentagone de côtés [AB] et [AE]. C et D complètent le pentagone régulier.

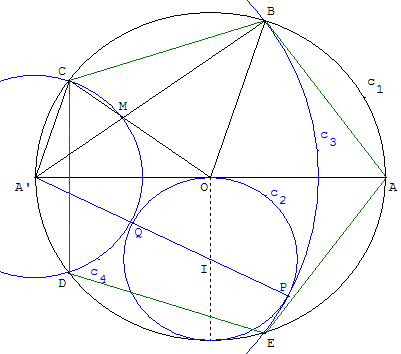
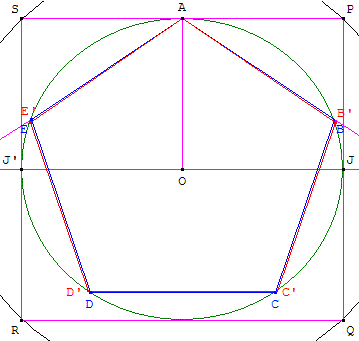
Placer deux points O et A et le cercle (c1) de centre O, passant par A, de rayon r.
O3 est le symétrique de A par rapport à O. B' est un des points d'intersection du diamètre perpendiculaire à [O3A] avec le cercle (c1).
K est le milieu du rayon [O3O].
Le cercle (c2) de centre K passant par B' coupe [OA] en U et [OO3) en T.
Le cercle (c3) de centre O3 passant par U coupe le cercle (c1) en B et E et la droite (O3A) en V.
Les droites (BV) et (EV) coupent le cercle (c1) en C et D.
Les points ABCDE sont les sommets du pentagone cherché.
Démonstration
Comme pour la méthode précédente B'U = AB, côté du polygone convexe et B'T = BE côté du pentagone croisé.
On a aussi : O3U = Φr =
![]() r ainsi que O3B et O3E rayons du cercle (c3).
r ainsi que O3B et O3E rayons du cercle (c3).
Dans le cercle (c1) le triangle O3BA inscrit dans un demi-cercle est rectangle en B.
cos AÔ3B =
![]() =
=
![]() =
=
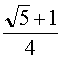 =
cos
=
cos
![]() .
Les angles aigus du triangle sont donc
.
Les angles aigus du triangle sont donc
![]() et
et
![]() .
.
L'angle BÂE est égal à
![]() .
Les deux segments égaux [AB] et [AE] sont deux côtés d'un pentagone régulier
inscrit dans le cercle (c1).
.
Les deux segments égaux [AB] et [AE] sont deux côtés d'un pentagone régulier
inscrit dans le cercle (c1).
Le triangle isocèle O3BU a un angle au sommet égal à
![]() ,
c'est un triangle d'or de côtés O3B = Φ r et BU = r.
,
c'est un triangle d'or de côtés O3B = Φ r et BU = r.
Dans le cercle (c3) l'angle inscrit
![]() correspond à l'angle au centre EÔ3B = 2 AÔ3B =
correspond à l'angle au centre EÔ3B = 2 AÔ3B =
![]() .
Cet angle inscrit est donc
.
Cet angle inscrit est donc
![]() =
=
![]() .
.
Les angles aigus du triangle VBA mesurent
![]() et
et
![]() .
Le troisième angle est
.
Le troisième angle est
![]() =
=
![]() .
Le point C est aussi un sommet du pentagone. Même démonstration pour D, ce qui
permet de conclure que ABCDE est un pentagone régulier.
.
Le point C est aussi un sommet du pentagone. Même démonstration pour D, ce qui
permet de conclure que ABCDE est un pentagone régulier.
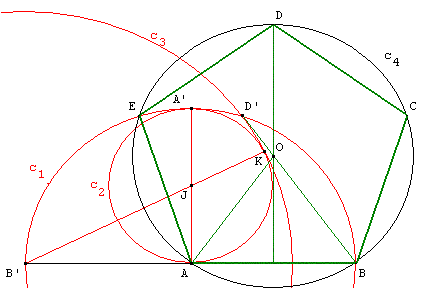
Dessin à partir d'un côté du pentagone : les points libres sont deux sommets consécutifs A et B.
Placer les deux premiers points A et B du polygone,
placer le point B' symétrique de B par rapport à A,
tracer le cercle (c1) de centre A passant par B (diamètre [B'B]),
la perpendiculaire en A à (AB) coupe le cercle C1 en A'.
Soit (c2) le cercle de diamètre [AA'] : son centre J est le milieu de [AA'].
Tracer la droite (B'J), cette droite coupe le cercle (c2) au point K.
Tracer le cercle (c3) de centre B' passant par le point K,
les cercles (c1) et (c3) se coupent en D', tracer le segment [BD'].
La médiatrice de [AB] coupe le segment [BD'] en O : O est le centre du cercle
circonscrit (c4) au pentagone et on peut vérifier que l'angle
AÔB mesure
![]() .
.
Pour tracer le pentagone régulier ABCDE, il suffit de placer le point C symétrique de A par rapport à (OB), un point E intersection des cercles (c1) et (c4), le point D est un des points d'intersection du cercle circonscrit (c4) et de la médiatrice de [AB] qui passe par O.

Dessin à partir d'un côté du pentagone : les points libres sont deux sommets consécutifs A et B.
Tracer le cercle (c) de centre A passant par B. Soit R un des points
d'intersection entre le cercle (c) et la droite perpendiculaire à (AB)
passant par A.
Soit I le milieu de [AB]. Le cercle de centre I passant par R coupe la
demi-droite [BA) en S.
Le cercle de centre B passant par S coupe le cercle (c) en E.
Il coupe aussi la médiatrice de [AB] en D.
Les segments [BA], [AE], [ED] sont trois côtés consécutifs du pentagone
régulier.
Tracer le cercle de centre D passant par E, puis celui de centre B passant par
A.
Seul un des points d'intersection de ces deux cercles permet d'obtenir un
polygone convexe : le point C.
ABCDE est un pentagone régulier.
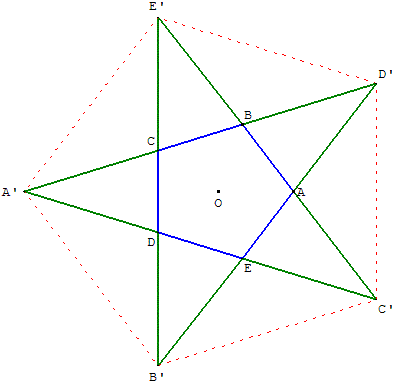
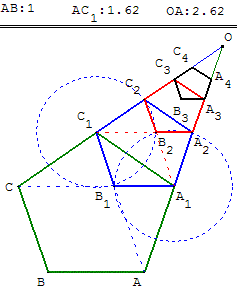
Soit ABCC1A1 un pentagone régulier. On note c la longueur du côté de ce pentagone et d la longueur de la diagonale. Soit B1 le point d'intersection des diagonales (AC1) et (A1C). Les points A1, B1 et C1 sont les sommets du pentagone régulier A1B1C1C2A2 de côté B1C1 = AC1 - AB1 = d - c et de diagonale A1C1 = c.
Comme tous les pentagones réguliers sont semblables on a :
d / c = AC1 / AA1 = A1C1 / B1C1 = c / (d - c).
Prendre c = 1 en choisissant la longueur AB comme unité. On a alors d = 1 / (d-1) soit d2 - d +1 = 0.
La solution positive de cette équation est le nombre d'or Φ =
![]() .
.
Dans tous les cas d = c Φ. Le pentagone A1B1C1C2A2
est l'image du pentagone ABCC1A1 par l'homothétie de
centre O et de rapport
![]() .
.
Si AA1 = 1, A1A2 =
![]() = Φ - 1; AA2 = 1 +
= Φ - 1; AA2 = 1 +
![]() = Φ.
= Φ.
Quand on itère cette homothétie on obtient une suite infinie de pentagones.
Observer la suite des points A, A1, A2, ...
A2A3 =
![]() = - Φ + 2, A3A4 =
= - Φ + 2, A3A4 =
![]() = 2Φ -3, A4A5 =
= 2Φ -3, A4A5 =
![]() = -3Φ + 5 et ainsi de suite ;
= -3Φ + 5 et ainsi de suite ;
voir TI-92 :
nombre d'or et suite de Fibonacci.
AAn = AA1 + A1A2 + A2A3
+ ... + An-1An, somme des premiers termes
d'une suite géométrique de raison
![]() ,
converge vers AO = 1 + Φ.
,
converge vers AO = 1 + Φ.
Placer deux points A et B. À partir de ce segment [AB] qui sera un côté du
pentagone on trace cinq cercles de même rayon :
Tracer les cercles de centre A passant par B et de centre B passant par A. Ces
deux cercles se coupent en P et Q.
Le cercle de centre P passant par A (et par B) coupe les deux premiers cercles
en R et S, et le segment [PQ] en G.
La droite (SG) coupe le premier cercle en E (voir figure) et (RG) coupe le
deuxième cercle en C.
Le dernier point D se trouve à l'intersection des cercles de centre E passant
par A et de centre C passant par B.

Le pentagone ABCDE a ses cinq côtés égaux. L'erreur sur les angles est d'un demi-degré à un degré et demi. Le point D est très légèrement en-dessous du point exact D' du pentagone régulier.

AbId est une feuille au format A4 (ou An). Ab = Ib
![]() .
.
[AI] étant une diagonale, replier I sur A. Le pli est le segment [ef]. Le point b se place en b'. Plier ensuite [b'e] sur la diagonale [AI] en plaçant b' en b1. De même plier [df] sur la diagonale [AI] en plaçant d en b1.
ABCD est pentagone presque régulier tel que tan IÂB = b'I/Ib' =
![]() ce
qui correspond à un angle d'environ 54,8° supérieur au 54° degrés attendus.
ce
qui correspond à un angle d'environ 54,8° supérieur au 54° degrés attendus.

Construction d'un pentagone de centre O et de sommet A. Voir les figures ci-dessus.
Expliquer pourquoi cette figure n'est qu'une construction approchée du pentagone régulier :
Dans le triangle rectangle OAI, tan OÂI = OI / OA =
![]() . Le
point B est très légèrement en-dessous du point exact B' du pentagone
régulier.
. Le
point B est très légèrement en-dessous du point exact B' du pentagone
régulier.
 |
 |
Cette construction d'un pentagone presque régulier est attribuée au mathématicien et philosophe grec Thalès de Milet (vers 600 avant J.-C.). Elle nécessite la règle et deux ouvertures de compas.
Deux points A et A1 étant donnés, tracer le cercle (c) de diamètre [AA1]. Les cercles de centres A et A1 et de rayon AA1 se coupent en P et Q.
On divise le diamètre [AA1] en n = 5 parties égales.
Les droites (PI2) et (PI4) rencontrent le cercle (c) en B et C, sommets du polygone. Ici on le complète par symétrie par rapport à (AA1). On obtient les points D et E intersections du cercle (c) et des droites (QI4) et (QI2).

Cette construction s'applique à un polygone régulier de n côtés. Elle est d'une grande facilité et d'une précision très satisfaisante jusqu'à n = 10.
Tracer les points libres M et N, puis le carré MNPQ. Le cercle de centre M
passant par P coupe la demi-droite [MN) en O.
La droite (OQ) coupe la diagonale [MP] du carré en C
Le cercle de centre O passant par C coupe [MN] en B. [BC] est un premier côté du
pentagone.
Le cercle de centre B passant par C coupe [NM) en A, point du pentagone.
Le cercle de centre C passant par B coupe [CQ) en D, quatrième point du
pentagone.
On termine le pentagone en trouvant l'intersection E des cercles de même rayon
de centres A et D.
Le pentagone ABCDE a ses cinq côtés égaux. L'erreur sur les angles est de un à deux degrés.
