DES QUESTIONS D’ORIGINES


Avertissement : la plupart des explications avancées ici, bien qu’issues des sources citées en bibliographie, ne sont que des hypothèses, parfois transmises comme des légendes de livre en livre.

LEXIQUE (utiliser rechercher dans la page) :

abscisse / affine / algèbre / algorithme / anneau / appartenance / alterné (groupe) / arithmétique /  arobase
C / cavalière (perspective) / corollaire / corps
e / ecart-type / ellipse / ensemble / ensemble vide / entière (série, fonction) / équilatéral
gamma (fonction) / géométrique / grand O / groupe
harmonique / homographique / huitante / hyperbole / hypergéométrique / inclusion / infini / intégral / intégration par parties / isocèle
ker / logarithme / mathématique / modulo / N / nabla / nonante / normal / noyau / numérateur / ordinateur / ordonnée / orthogonal
parabole / parallélépipède / parallélogramme / petit o / pgcd / ppcm / pi / pourcentage
Q / quantificateur / R / radian / radical / rationnel / régression /sens trigonométrique / septante / sinus / symétrique (groupe) / théorème / Z
 

1) Des mots bizarres

Pourquoi des « mathématiques » ?

Le mot « mathématique » comme aussi celui de « philosophie » serait dû à Pythagore. Il provient du grec mathêma qui veut dire « science » dans l’optique de l’époque, c’est-à-dire « toute la connaissance ». Mathêmatika en grec comme mathematica en latin sont des pluriels, c’est pourquoi on dit des mathématiques. Certains essaient de parler de la mathématique, pour montrer son unité, mais cela ne prend pas. Notons qu’en anglais on dit mathematics avec un s, mais que c’est un mot singulier…

Théorème est-il apparenté à théologie ?

Non, il est plutôt apparenté à « théâtre ». La première syllabe ne vient pas de theos « dieu », mais de thea « spectacle ». Comme le mot « théorie », le mot « théorème » a été construit à partir du verbe grec theorein signifiant « observer ».

Corollaire est-il apparenté à corolle ?

Oui ; ces deux mots vienne du latin corolla qui signifiait « petite couronne » ; l’on donnait en effet une petite couronne de lauriers aux acteurs comme gratification. Un corollaire est donc un cadeau donné en plus par le théorème !

Pourquoi des nombres « rationnels » ?

Les nombres rationnels ne sont pas dénommés ainsi parce qu’ils seraient plus rationnels que les autres, comme je l’ai longtemps cru. L’étymologie latine ratio n’est pas ici à prendre dans le sens de raison mais dans celui de rapport, quotient (cf. le mot français « ratio ») : les nombres rationnels sont les nombres quotients de deux entiers. C’est l’écrivain latin Cassiodore (498 – 575) qui aurait utilisé cette dénomination pour la première fois.

L’expression « entier rationnel », pour entier relatif peut alors paraître bizarre, mais elle est à prendre dans le sens : « élément entier de l’anneau des rationnels ». De même, « fraction rationnelle », qui peut apparaître pléonastique, est apparu après « fonction rationnelle », ratio de deux polynômes.

Pourquoi un numérateur et un dénominateur ?

Le dénominateur dénomme, donne son nom à la fraction. Le numérateur, lui, indique le nombre de parties définies par le dénominateur.

Y a-t-il un rapport entre la fonction sinus et les sinus du front ?

Oui et non ; le mot « sinus » est un mot latin signifiant « courbe, pli, cavité ». Il a donné en français les mots « sein » (d’ailleurs, en italien, le sinus mathématique se dit seno, qui signifie aussi « sein ») et « sinueux ». Mais si les sinus du front forment bien des cavités, l’interprétation selon laquelle le sinus mathématique s’appellerait ainsi car une sinusoïde est sinueuse est un contresens, car la notion de représentation d’une fonction est bien plus récente que celle de sinus !

Voici l’histoire probable du mot « sinus », qui vient d’une erreur de traduction.

Quant au cosinus, c’est tout simplement le sinus du complémentaire (de l’angle) ; « co- » vient du latin cum, qui signifie « avec ».

La tangente, elle, vient de ce qu’elle mesure une portion d’une tangente au cercle trigonométrique ; et la cotangente est aussi la tangente du complémentaire.

Pourquoi des « logarithmes » ?

Le terme a été créé en 1614 par le mathématicien écossais John Napier (francisé en Néper), à partir des mots grecs logos pouvant signifier « rapport » et arithmos « nombre ».  Pour comprendre cette étymologie, il  faut savoir que Néper définit le logarithme comme le rapport de la distance à parcourir de deux mobiles, l’un se déplaçant à vitesse constante et l’autre à vitesse proportionnelle à la distance restant à parcourir. Le logarithme est alors le rapport de deux nombres. 

D’où vient le mot « algorithme » ?

Malgré son petit air grec, ce mot, comme beaucoup commençant par al (comme « alcool »), vient de l’arabe. Al-Khwarizmi est le surnom du mathématicien Abu Ja’far Mohammed Ben Musa (c. 780 – c. 850), originaire de la région du Khwarazm (actuellement Khiva en Ouzbékistan), d’où son surnom. L’un de ses livres d’arithmétique a été traduit en latin sous le nom de liber algorismi (« livre d’Al-Khwarizmi »). Du coup, on a désigné par algorismus le système de numération décimal, puis c’est devenu en français « algorithme » avec un sens plus général, par l’influence du mot arithmos (« nombre » en grec) et de « logarithme » qui en est une anagramme.

Et le mot « algèbre » ?

Encore un mot d’origine arabe, commençant par al (« le » en arabe). Il provient de la première partie du titre d’un livre du mathématicien Al-Khwarizmi, dont nous venons de parler : Al jabr w’al muqabalah, signifiant « la remise en place et la simplification ». La remise en place en question est le passage des éléments négatifs d’une équation de l’autre côté du signe égal pour les rendre positifs : voilà le point de départ de l’algèbre. Vous pourrez d’ailleurs voir dans un dictionnaire espagnol que algebrista ne signifie pas « algébriste », mais « rebouteux » : en effet, celui-ci remet en place les membres luxés !

Pourquoi une « abscisse », une « ordonnée » ?

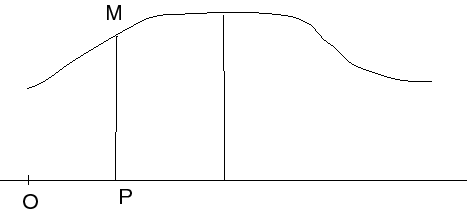
Ces deux noms sont des adjectifs substantivés, abréviation de « ligne abscisse (c’est-à-dire « coupée », cf. « scission ») et lignes ordonnées ». Historiquement, l’ordonnée est apparue avant l’abscisse ; étant donnée une courbe décrite par un point M et une droite (D), les ordonnées étaient les segments [MP] où P est le projeté de M sur (D) ; ces segments étant disposés régulièrement, de façon ordonnée (= ordinatim en latin), ont été appelés ordinatim applicatae en latin, puis ordonnées en français.

Étant donné un point O sur D, les abscisses étaient les segments [OP], qui sont bien des « lignes coupées ».

abscisses et ordonnées

Le mot « ordonnée » serait apparu en premier sous la plume de Pascal en 1658 et le mot « abscisse » (sous sa forme latine abscissa) en 1692 dans un texte de Leibniz.

Notons que Descartes n’a jamais utilisé aucun de ces deux termes !

Ce serait Euler (1707 – 1783) qui aurait le premier détecté la symétrie existant entre les notions d’abscisse et d’ordonnée.

D’où vient le mot « radian » ?

Du latin radius, qui signifie rayon (cf. « radial »). Mais pourquoi rayon ? Car un angle d’un radian intercepte un arc de cercle dont la longueur est égale au rayon du cercle !
Le terme a été employé pour la première fois par Thomson en 1873.

Radian

Que sont ces « cèle », « pipède » et « gramme » dans isocèle, parallélépipède, et parallélogramme ?


D'où vient l'expression « modulo n » ?

Modulo est l'ablatif du mot latin modulus signifiant mesure ; modulo n signifie donc "à la mesure de n". L'expression a été introduite par Gauss en 1801.

Pourquoi les coniques s’appellent-elles ellipse, parabole et hyperbole ?

Les mots « ellipse, hyperbole et parabole » ont été transcrits par Johannes Kepler (1571-1630) des mots grecs elleipsis, huperbolê et parabolê, noms qui avaient été donnés par Aristée (IVe siècle avant J.C.) et popularisés par Apollonius de Perge (env. 262 – 190 av. J.C.).

Le mot grec elleipsis a été créé à partir du verbe elleipein qui signifie « manquer » (« éclipse » a la même origine), tandis que huperbolê et parabolê sont des mots grecs existant signifiant l’un « excès » et l’autre « ressemblance » ou « juste adéquation ». Le suffixe bolê vient du verbe ballein signifiant « lancer », (cf. le « discobole » et la « balistique »). Remarquons que pour une parfaite symétrie, Aristée aurait pu créer « hypobole » pour ellipse !

Les trois mots « ellipse », « parabole » et « hyperbole » représentent aussi des figures de rhétorique, en bonne adéquation avec leur étymologie : une ellipse est une formule raccourcie (comme « chacun son tour » à la place de « chacun doit attendre son tour »), une parabole est un récit allégorique, une hyperbole est une formule exagérée (comme « mourir de rire »).

En mathématiques, une ellipse manque aussi de quelque chose, une hyperbole présente un excès, mais de quoi ? C’est là que les réponses divergent...

Pour le dictionnaire historique de la langue française, une ellipse manque... de perfection par rapport à un cercle. Bien que plausible, cette interprétation tue la symétrie ellipse – hyperbole, autour de la parabole.

On peut aussi penser que la raison vient de ce que sur une ellipse la distance au foyer est plus petite que la distance à la directrice (excentricité e < 1) , sur une parabole, elle est égale (e = 1) et sur une hyperbole, elle est supérieure (e > 1), mais c’est un contresens car les Grecs ne connaissaient pas la définition à partir des foyers et des directrices.

Plus sûre est l’interprétation suivante, car pour les Grecs, les coniques sont des sections de cône. On considère la section d’un cône par un plan perpendiculaire à une génératrice :

Une deuxième explication peut provenir du fait que, en écriture moderne, l’équation générale réduite d’une conique est , l’ellipse, la parabole et l’hyperbole étant obtenues pour respectivement  (en fait ).

On lit sur cette équation que l’aire du carré construit sur l’ordonnée est égale à l’aire du rectangle défini par l’abscisse et la corde passant par le sommet, aire à laquelle il faut retirer ou ajouter une certaine aire suivant que l’on a une ellipse ou une hyperbole, l’égalité avant lieu pour la parabole ; ceci se trouve dans le livre d’Apollonius sur les coniques.

Lorsqu’on applique le carré y² sur le rectangle 2px, le carré est en défaut dans le cas de l’ellipse (c’est le sens du terme grec ellipse), en excès dans le cas de l’hyperbole (c’est le sens du terme grec hyperbole), le terme parabole signifiant l’égalité des aires.

Pourquoi des progressions, suites et moyennes arithmétiques, géométriques et harmoniques ?

Rappelons que des nombres sont en progression arithmétique si la différence de deux termes consécutifs est constante (comme 8, 12, 16, 20), en progression géométrique si le rapport de deux termes consécutifs est constant (comme 8, 12, 18, 27) et en progression harmonique si les inverses sont en progression arithmétique (comme 3, 4, 6, 12) ; dès lors, une suite est arithmétique, géométrique, harmonique si ses termes sont en progression arithmétique, géométrique, harmonique et c est la moyenne arithmétique, géométrique, harmonique de a et b si les nombres a, c, b sont en progression arithmétique, géométrique, harmonique.

Ces qualificatifs « arithmétique, géométrique, harmonique » sont très anciens : ils sont dus aux pythagoriciens, au sixième siècle avant Jésus-Christ.

L’expression « arithmétique » est probablement due au fait que les entiers naturels 1, 2, 3, 4, (arithmos en grec) forment la plus simple des suites arithmétiques.

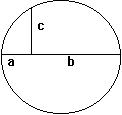
L’expression « géométrique » provient plutôt de la moyenne géométrique dont la définition naturelle est de nature géométrique : la moyenne géométrique de a et b, est le côté c du carré qui a même aire que le rectangle de côtés a et b. Et ce nombre s'obtient par une construction à la règle et au compas très simple :

moyenne géométrique

L’expression « harmonique » est probablement à rattacher à la suite des inverses des naturels qui est la plus simple des suites harmoniques. Cette suite (1/n) s’introduit naturellement en musique : si une corde de longueur l vibre à une fréquence f, une corde (de même masse linéique et de même tension) de longueur l/2, l/3, l/4... vibrera aux fréquences 2f, 3f, 4f... qui sont les « harmoniques » de f.
Autre possibilité : la moyenne harmonique de 1 et 2 est 4/3 et la succession 1 ; 4/3 ; 2, envisagée comme une succession de fréquences, correspond aux notes do - sol - do dans la gamme pythagoricienne.

On peut ajouter que si le terme « raison » (du latin ratio, « rapport ») se justifie bien dans le cas des suites géométriques, où il désigne le rapport constant d’un terme au précédent, ce n’est pas le cas – sinon par analogie – pour une suite arithmétique, où il désigne la différence constante entre un terme et le précédent.

Pourquoi le calcul « intégral » ?

Ce terme provient du latin integer « entier, total », probablement car une intégrale est le rassemblement (l’intégration !) d’une infinité de termes infinitésimaux en un tout. Le terme est du mathématicien suisse Jacques Bernoulli en 1696 ; Leibniz aurait préféré au départ le terme calcul « sommatoire » mais a été convaincu par Jean Bernoulli, frère de Jacques ; en échange, le signe d’intégration est issu de la lettre S, et non de la lettre I...

Pourquoi  est-elle une intégration « par parties » ?

Je ne sais pas... Peut être parce qu’on n’intègre qu’« en partie » , ou que l’intégrale est séparée en deux parties ?

Pourquoi une fonction « homographique » ?

Je ne dois pas être le seul à avoir longtemps pensé que les fonctions homographiques x |–> (ax + b) / (cx + d) s’appellent ainsi car elles ont toutes des graphiques semblables (une hyperbole d’asymptotes parallèles aux axes). En fait leur nom provient de ce que les transformations du même type de C dans C : x |–> (az + b) / (cz + d) transforment les figures du plan en des figures similaires (elles transforment des cercles ou droites en des cercles ou droites). Le terme est du à Michel Chasles (1793-1880).

Porquoi des séries « entières » ?

Ce qui est entier dans une série entière , ce sont les exposants n ; l'expression : "série de puissances entières positives" s'est bizarrement abrégée en "série entière" en France, et "série de puissances" en anglais, en allemand, en espagnol et en italien (power series, Potenzreihe, serie de potencias, serie di potenze). Quant aux fonctions entières, elles sont ainsi nommées car elles sont holomorphes dans le plan tout entier.

 

Pourquoi parle-t-on de loi « hypergéométrique » ?


La loi hypergéométrique est la loi du nombre B de boules blanches dans un tirage sans remise de r boules parmi p boules blanches et q = n - p boules noires. Elle est définie par  ; alors pourquoi est-elle hypergéométrique ?
Parce que sa série génératrice E(xB) est un cas particulier de série hypergéométrique.

Et pourquoi les séries hypergéométriques s'appellent-t-elle ainsi ?

Car elles généralisent la série géométrique ; c'est le mathématicien Pfaff, maître et ami de Gauss, qui a introduit ce terme.

Détails techniques : une série entière  est dite hypergéométrique si  est une fraction rationnelle en n.
Avec les notations de Maple,  où (a)n est la factorielle montante .
La série géométrique  est alors hypergeom( [1], [ ], x ), et la fonction génératrice de la loi hypergéométrique est 

Pourquoi normal veut-il dire (parfois) orthogonal ?

Parce que ce mot vient du latin normalis signifiant équerre. C’est donc le sens premier de ce mot. Le mot « normé » vient de « norme » ayant pris le sens de « canon, modèle ». C’est pourquoi il vaut mieux parler de base orthonormée que de base orthonormale !

Pourquoi un écart-type ?

Le terme est une traduction de l’anglais standard deviation, introduit par l’Anglais Karl Pearson en 1893.

Pourquoi une droite de régression ?

L'expression est dûe à F. Galton en 1885. Dans son ouvrage "Regression towards mediocrity in hereditary stature", son étude statistique montrait que des parents de taille fortement diférente avaient des enfants dont la taille tendait à régresser vers la moyenne. Et il désigne par droite de régression la droite décrivant la relation entre la taille des parents et celle des enfants.

Pourquoi des perspectives cavalières ?

Une perspective cavalière est une perspective où les parallèles restent parallèles (contrairement à une perspective conique où les droites parallèles deviennent en général concourantes) ; elle est obtenue théoriquement pour un observateur situé à l’infini. Une origine possible de l’expression « perspective cavalière » est qu’un cavalier regardant du haut de son cheval un objet à terre le voit quasiment en perspective cavalière. Le terme datant du XVIe siècle où il était utilisé en architecture militaire, une autre interprétation proviendrait du fait qu’un cavalier est, en matière de fortification, un haut monticule de terre. La vue cavalière est alors la vue qu’a sur la campagne, un observateur situé sur le haut du cavalier ; la perspective cavalière serait donc le procédé utilisé par le dessinateur de fortifications pour rendre la vue cavalière.

Par contre l’interprétation disant que l’expression viendrait du mathématicien Cavalieri est fantaisiste.

Pourquoi dit-on un PGCD et non un PGDC (plus grand diviseur commun), un PPCM et non un PPMC (plus petit multiple commun) ?

Réponse plausible non vérifiée : l'adjectif "commun" se plaçait autrefois avant le nom, comme en témoigne l'expression : aucune commune mesure. On peut aussi remarquer que ppcm est plus facile à prononcer que ppmc..

Pourquoi un espace « affine » ?

Le terme vient d’affinité, introduit par Léonard Euler en 1748, qui remarque (en français dans le texte) que deux courbes obtenues l’une de l’autre en changeant l’échelle des abscisses ne sont pas semblables, mais qu’elles ont quand même une certaine « affinité ». Mais nous ne savons pas qui a introduit l’utilisation de l’adjectif « affine ». Peut-être est-ce à cause d’un détour par l’anglais que ce mot qui devrait être « affin » au masculin est devenu affine ?

Pourquoi des ensembles, des groupes, des anneaux, des corps ?

« Ensemble », « groupe » et « corps » ont le sens de « regroupement d’individus », avec une cohésion croissante (pour « corps », penser à « corps de métier, corps diplomatique »). Seul anneau semble faire exception, mais ce mot est traduit de l’allemand Ring qui signifie aussi dans cette langue « cercle » (comme dans « cercle philatélique »). Notons que si les ensembles s’appellent généralement E, les groupes G, et les anneaux A, les corps sont désignés par K, car corps se dit en allemand Körper. Dans un texte anglais, ils seront désigné par F, car corps se dit field (= « champ »). Le mot « ensemble » est probablement dû à l’Allemand Georg Cantor en 1883 (sous sa forme allemande de Menge qui signifie aussi « foule »), le mot « groupe » au Français Évariste Galois en 1830, les mots « anneau » et « corps » (sous la forme Ring et Körper) à l’Allemand Richard Dedekind en 1871 dans son livre : Lehrbuch des Algebra.

Pourquoi les groupes symétrique et alterné s'appellent-ils ainsi ?

Le groupe symétrique associé à n objets x1, ..., xn est le groupe de leurs permutations, et le groupe alterné en est le sous-groupe formé des permutations paires. Une fonction symétrique de ces n objets est par définition invariante lorsqu'on permute deux de ces objets, et donc aussi par toutes les permutations du groupe symétrique ; une fonction alternée est par contre une fonction qui change de signe quand on permute deux objets : le groupe des permutations laissant invariantes les fonctions alternées est donc le groupe des permutations paires.
Le groupe symétrique est associé aux fonctions symétriques, le groupe alterné aux fonctions alternées : voilà l'explication.

Septante, huitante (ou octante) et nonante.

Ce sont nos soixante-dix, quatre-vingts et quatre-vingt-dix pour les Suisses et les Belges, issus des mots latins septuaginta, octoginta, nonaginta.

Grevisse (Le bon usage, p. 926) dit que Vaugelas a condamné septante et nonante comme des archaïsmes, mais en fait il semblerait que ce soit plutôt le contraire !

Une hypothèse non vérifiée est que soixante-dix, quatre-vingts et quatre-vingt-dix sont justement des archaïsmes issus du gaulois, langue celte, comme le breton. Le système vigésimal est en effet net en breton où 20 se dit ugent, 40 daou-ugent, 60 tri-ugent, 70 dek ha tri-ugent (c’est-à dire 10 plus 3 fois 20) etc. Et ceci proviendrait de langues pré-indo-européennes utilisant un système vigésimal (c’est-à dire de base 20). par exemple, en basque, 20 se dit hogei, 30 hogeitabat (20 + 10), 40 berrogei (2 fois 20), 60 hirurogei (3 fois 20) etc. En Europe, on trouve encore le danois où 50 se dit halvtredsce qui signifie (3-½)*20, 60 : tres = 3*20, 70  halvfjerds = (4-½)*20, 80 : firs = 4*20 et 90 : halvfems = (5-½)*20. On trouve aussi une trace de base 20 dans le nom du très célèbre hospice des « Quinze-Vingts » datant de 1254, ainsi nommé pour loger 300 vétérans aveugles.
 

Et c’est l’hégémonie francilienne qui a imposé récemment ces archaïsmes à toute la France (on disait encore septante et nonante il y a cinquante ans dans le sud et le sud-est). Les Suisses et les Belges (dont les dialectes ne connaissent pas la base 20) ont résisté !

Notons que si la plupart des peuples comptent en base 10, c’est à cause de nos 10 doigts ; ceux qui comptent en base 20 ont aussi inclus les orteils…
Sur le sujet, voir deux pages bien plus détaillées :
monsu.desiderio.free.fr/curiosites/vingt.html et monsu.desiderio.free.fr/curiosites/septante.html

Pourquoi dit-on un ordinateur ?

Le français est, avec l'espagnol, la seule langue où l’on dit « ordinateur », et non « calculateur ». Ce mot, qui se trouve dans le Littré comme adjectif désignant « Dieu qui met de l’ordre dans le monde » a été proposé non par un scientifique, mais par le philologue Jacques Perret, en 1955, à IBM France, et a été retenu contre l’anglicisme « computeur » (impossible en français à cause de « con » et « pute » !).

2) Des symboles bizarres

Pourquoi le nombre  s’appelle-t-il ainsi ?

L’utilisation de la lettre grecque  pour le rapport de la circonférence au diamètre a été popularisée par Léonard Euler dans un ouvrage sur les séries publié en latin en 1737 ; mais elle est due au départ à un mathématicien anglais, William Jones, qui l’a utilisée dans un livre paru en 1706. Cependant, en 1647, le mathématicien anglais William Oughtred avait déjà utilisé p pour désigner le périmètre d’un cercle (et non son rapport au diamètre). La lettre p est à la fois l’initiale de periphereia et de perimetros qui en grec désignent la circonférence d’un disque.

Et le nombre e ?

Tout le monde avait trouvé : c’est l’initiale d’exponentielle. Mais il y a fort à parier qu’Euler, en utilisant cette notation pour la première fois en 1728, à l'âge de 21 ans, dans un livre sur les canons, n’était pas sans avoir avait remarqué que c’était aussi l’initiale de son nom !

Et le nombre d'or j ?

C'est l'initial du sculpteur Phidias qui décora le Parthénon, dont la façade est un rectangle d'or, et non la transcription grecque de la première lettre de Fibonacci, comme je le pensais...

Et la fonction G ?

La notation est due à Adrien Legendre en 1811 ; on pense qu'il a simplement retourné l'initiale de son nom de famille. Binet a fait mieux en 1839 ; il a désigné par le correspondant grec de l'initiale de son nom une fonction, et ce nom est resté (la fonction b).

D’où vient le symbole % ?

Au XVe siècle, les Italiens écrivaient Pc° pour per cento. C’est devenu petit à petit Ps° puis PImage ensuite, le P a disparu et le symbole est devenu l’actuel %. Les deux faux zéros de ce symbole ont petit à petit été assimilés aux deux zéros de 100 ; c’est pourquoi on a rajouté un zéro pour écrire ‰.

D’où vient le symbole des radicaux  ?

Ce symbole est dû à l’Allemand Christoff Rudolff en 1525, dans son ouvrage die Coss. C’est probablement un r minuscule déformé, initiale de « racine » (radix en latin). 

D’où vient le symbole d’intégration ?

Ce symbole est dû à Gottfried Wilhelm Leibniz (1646 – 1716). C’est un S allongé, car une intégrale est une somme (summa en latin).

D’où vient le symbole de l’infini  ?

Ce symbole est dû à John Wallis qui l’a introduit en 1655 ; il se trace comme un huit couché mais son origine n’est pas le symbole 8. Ce symbole viendrait : Il est aussi probable que J. Wallis a pensé au fait que la courbe de même forme (la lemniscate) se parcourt sans fin.

Pourquoi l’appartenance se note-t-elle  et l’inclusion  ?

C’est le symbole d’inclusion qui est apparu le premier sous la plume de Gergonne en 1816 mais semble-t-il dans le sens contraire du sens actuel ; on peut penser qu'il l’a défini à partir de la lettre C, l’initiale de "Contient", de sorte que AB était simplement une abréviation de A Contient B ; c'est Schröder qui a utilisé pour la première fois  et  dans leurs sens actuels, probablement par déformation de < et  > .

Le symbole d’appartenance est, lui, issu de la lettre grecque epsilon, qui est l’initiale de  (esti) signifiant « (il) est ». Il a été créé par Peano en 1890.

D’où viennent les symboles des quantificateurs  et  ?

Le premier apparu historiquement est le quantificateur existentiel , qui se lit aujourd'hui : « pour au moins un » ou « il existe au moins un… tel que » ; c'est Peano qui, dans son "formulaire de mathématiques" publié en français en 1897 a eu l'idée de retourner droite-gauche un E, initiale d' "Exister".

Il a fallu 40 ans pour que Gentzen ait l'idée en 1935 de retourner haut-bas un A, initiale de All qui signifie « tout » en allemand et en anglais, pour désigner le quantificateur universel , qui se lit maintenant « pour tout » ou « quel que soit » et de formaliser par là-même la dualité entre" pour tout" et "pour au moins un".
Si un français y avait pensé avant, on aurait un un T à l'envers, et on serait bien embêtés pour l'orthogonalité !

D’où vient le nabla  ?

Ce symbole introduit par William Hamilton en 1853 est tout simplement un delta majuscule renversé, d’où son nom parfois donné d’« atled ». Il ressemble à une lyre, c’est pourquoi  Heaviside l’a appelé nabla, mot grec d’origine phénicienne désignant justement une sorte de lyre en forme de delta renversé. En hébreu, harpe se dit nebel…
  nabla = lyre !

Pourquoi petit o et grand O ?

Ces symboles sont connus sous le nom de notations de Landau (1877-1938). Le o est l’initiale de l’allemand Ordnung qui signifie « ordre ». Il s’agit en effet de comparer les ordres de grandeurs de fonctions au voisinage d’un point.

Pourquoi  ?

désigne l’ensemble des entiers naturels, baptisés ainsi en 1763 par William Emerson, suite à Nicolas Chuquet parlant de « progression naturelle » pour la suite 1, 2, 3, 4... C’est l’Italien Giuseppe Peano (1858-1932) qui a utilisé la lettre  pour leur ensemble (naturale en italien) ; dire que  est l’initiale de « nombre » est donc un contresens.

Par contre,  est bien l’initiale de nombre... en allemand (Zahl) ! Cette appellation est due à l’Allemand Richard Dedekind (1831-1916). Ceci n’empêchera pas les profs de maths de dire aux élèves que c’est l’ensemble des « zentiers »…

est l’ensemble des nombres rationnels, baptisés ainsi par Cassiodore (voir ci-dessus) ; c’est Peano qui a utilisé la lettre  pour leur ensemble (quotiente = quotient en italien).

est l’ensemble des nombres réels, baptisés ainsi par Descartes en 1637 (en même temps qu’il désignait par imaginaires les autres nombres) ; c’est l’Allemand Georg Cantor (1845-1918) qui a désigné pour la première fois l’ensemble de ces nombres par  (« réel » = real en allemand).

est l’ensemble des nombres complexes, baptisés ainsi par Karl Friedrich Gauss en 1831 (en latin) reléguant les imaginaires aux nombres .

Et pourquoi ces ensembles sont-ils écrits avec des majuscules à double trait ?
C'est Bourbaki qui a rassemblé ces notations et les a fait imprimer en caractère gras. Cependant, au tableau noir, il est difficile de faire des caractères gras à la craie et de là est venue l'idée de doubler les traits. Par allez-retour, c'est devenu une police d'imprimerie à part entière, d'ailleurs naturellement appelée "blackboard bold" (gras pour tableau noir).

Pourquoi le symbole de l’ensemble vide est-il la lettre Ø des alphabets norvégien et danois ?

Parce qu’il fallait un symbole qui ressemble au 0 sans en être un et que le mathématicien du groupe Bourbaki André Weil qui l’a introduit en 1937 connaissait le norvégien.

Pourquoi un noyau se note-t-il Ker ?

Ker ne vient pas mot du breton signifiant « maison », mais de l’allemand Kern, signifiant tout simplement « noyau ». En anglais, le noyau se dit aussi kernel, signifiant "amande" dans le civil.

Quelles sont les origines du sens des aiguilles de la montre et du sens trigonométrique ?

Les montres et horloges ont repris les graduations des cadrans solaires horizontaux, ou gnomons, et le sens des aiguilles correspond à celui de l’ombre. Attention, dans les cadrans solaires verticaux, l’ombre tourne dans l’autre sens (et tout ceci ne vaut d’ailleurs que dans l’hémisphère nord !) : le 12 est en bas et le 1 juste à sa droite.

Le sens trigonométrique est lié à la manière dont on représente un repère Oxy, et cette représentation est probablement due à notre écriture de gauche à droite. On peut remarquer que c’est le sens de rotation de la terre autour du soleil, pour un observateur situé du côté du pôle nord terrestre, ainsi qu’au sens de rotation de la terre sur elle-même, pour un observateur placé au pôle nord.

La lune tourne aussi dans le sens trigonométrique autour de la terre et sur elle-même, pour un observateur placé au pôle nord terrestre. Même schéma pour la plupart des planètes et de leurs satellites.

D’où vient le symbole @ ?

Ce caractère était pratiquement inconnu en France il y a quelques années, mais a été popularisé par Internet. La date d'apparition dans le courriel est 1971.

Il était par contre courant en Angleterre et aux États-Unis en remplacement de at, comme l’esperluette & en remplacement de « et ». Exemple d’utilisation : What is the total cost of 5 apples @ 5 d ?

Comme l’esperluette (&), @ est issu des chancelleries ; c’est la ligature du latin ad (« à » en français) où le a et le cursifs de l’onciale ont fini par se confondre. Il constituait la première ligne d’adresse de documents diplomatiques.

Le nom français de ce caractère, est selon l’AFNOR « a commercial », comme le & est « et commercial ». Cependant, le nom que lui donnent les internautes français tourne autour de sa forme : « a-rabesque », « a-rondi », « a enroulé ». Mais le nom le plus fréquemment employé est « aroba », « arobase » ou « arrobas ». Il vient probablement d’une confusion : on trouve en effet dans les catalogues de fondeurs français un caractère qui a à peu près la même graphie que @, qui s’appelle « arobas », mais qui correspond à quelque chose de complètement différent : c’est le symbole d’une ancienne unité de poids et de capacité encore usitée en Espagne et au Portugal, arroba, équivalant à 12 à 15 kg ou 10 à 16 l, dont le vrai nom français est d’ailleurs « arrobe » ou « arobe ». Le mot provient de l’arabe arba signifiant « quatre ».

Une autre hypothèse est que « arobas » soit une déformation de « a rond bas (de casse) » : « a rond » pour le a dans un rond, et « bas de casse », désignant les lettres minuscules qui se trouvaient en bas de la casse, planche à casiers dans lesquels étaient classées les formes en plomb des lettres.

Ce site est beaucoup plus catégorique...

Bibliographie :