Quelques notions de thermodynamique
Notre sens commun nous a donné l’habitude de parler de deux formes d’énergie macroscopique : le travail mécanique et la chaleur. Cette dernière est liée à la notion de température qui est un paramètre macroscopique que nous connaissons tous. A notre échelle, travail et chaleur sont deux manifestations différentes de l’énergie. Ainsi, lorsque nous soulevons une valise, nous fournissons un travail (avec nos muscles), alors que si nous chauffons de l’eau dans une casserole, nous fournissons de la chaleur au fluide contenu dans le récipient.
La thermodynamique est cette branche de la Physique dont le principal but est de décrire les transformations entre ces deux formes d’énergie ; par essence, c’est une science qui s’applique aux corps macroscopiques. Ceux-ci sont à notre échelle et constitués d’un grand nombre de particules. La thermodynamique essaie donc de décrire les propriétés de ces corps, liées aux transferts d’énergie thermique ou mécanique, sans faire appel à leur structure microscopique. Cette description repose sur des variables macroscopiques (dites aussi thermodynamiques) telles que la température T, la pression P, le volume V, etc… et la plupart de ces variables ont été introduites grâce à l’observation de phénomènes physiques dont nous nous faisons tous une idée qualitative sinon quantitative.
1 - Le parler de la thermodynamique
On appelle système une partie de l’Univers entourée par une surface fermée. Celle-ci peut-être éventuellement fictive et n’est pas nécessairement fixe, mais elle délimite le système.
Exemple : le gaz enfermé dans un ballon constitue un système dont la paroi en caoutchouc représente la surface fermé délimitante. Selon la pression du gaz et la pression extérieure, cette surface varie.
Un système est isolé ou fermé s’il n’a pas d’interaction avec le reste de l’Univers ; il est ouvert dans le cas contraire. Un système véritablement fermé n’existe pas dans la nature car tout corps interagit, même très faiblement, avec le milieu extérieur. Il en existe néanmoins d’excellentes approximations lorsque les interactions sont suffisamment faibles pour être négligées.
Exemple : un liquide enfermé dans une bouteille Thermos (vase Dewar) est une bonne approximation de système isolé : il n’échange ni chaleur ni matière avec le milieu extérieur, pour autant qu’on le considère sur un laps de temps inférieur à quelques heures. En effet, ce système échange tout de même une très faible quantité de chaleur avec l’extérieur et, au bout d’un jour ou deux, le liquide se sera refroidi ou réchauffé en fonction des conditions extérieures.
En Physique, on essaie toujours de représenter des situations réelles par des modèles que l’on peut facilement traiter mathématiquement et qui permettent de décrire les phénomènes observés avec une bonne précision. Dans l’exemple précédent, l’approximation du système isolé est excellente si l’on considère le liquide pendant quelques minutes ; elle est très mauvaise si on l’observe pendant plusieurs jours et il convient alors de traiter le liquide comme un système ouvert.
En thermodynamique, on est souvent amené à considérer le système fermé constitué
de deux sous-systèmes en interaction, séparés par une paroi. Celle-ci est dite
adiabatique si elle ne conduit pas la chaleur. Dans la pratique,
on sait réaliser des parois qui conduisent mal la chaleur et qui sont une bonne
approximation de paroi adiabatique : c’est le cas, par exemple, du vase Dewar
des bouteilles Thermos ; la laine de verre ou le feutre sont également de bons
isolants thermiques utilisés à cette fin. Ces matériaux peuvent constituer
d’excellentes parois adiabatiques si l’on observe le système pendant un temps
qui n’est pas trop long comparé au temps nécessaire pour que les fuites
thermiques deviennent importantes. Si la paroi séparant les deux systèmes
conduit bien la chaleur, elle est dite diatherme. Une séparation de cuivre en
est une bonne approximation ; ce matériau est d’ailleurs utilisé pour réaliser
les semelles de nos casseroles.
Les propriétés thermodynamiques d’un système sont décrites à l’aide d’un petit nombre de variables macroscopiques ou thermodynamiques ; ces paramètres, qui peuvent être déterminés en effectuant des mesures à notre échelle, caractérisent l’état d’un système macroscopique. Ce sont par exemple la température absolue T, la pression P, le volume V, le nombre de particules N (ou la quantité de matière n = N/NA où NA est la constante d’Avogadro, NA = 6,021023 mol-1). Pour décrire complètement l’état thermodynamique d’un système, il faut connaître la valeur d’un certain nombre de variables macroscopiques. On appellera état macroscopique ou macroétat la configuration qui est associée à la valeur de ces paramètres. Un macroétat est donc complètement déterminé du point de vue de la thermodynamique.
Exemple : un gaz est dit parfait si l’interaction mutuelle entre les molécules qui le constituent est négligeable. L’hélium à basse pression en est une bonne approximation. Nous pouvons décrire complètement les propriétés thermodynamiques d’un gaz parfait avec quatre variables macroscopiques : T, P, V et n. Il suffit toutefois d’en connaître trois pour déterminer la quatrième puisqu’elle sont reliées par l’équations d’état des gaz parfaits
PV = nRT
où R est la constante des gaz parfaits : R = 8,314 J.K-1.mol-1.
Une équation d’état exprime la propriété selon laquelle toutes les variables macroscopiques caractérisant un système ne sont pas indépendantes.
Un système est dit en équilibre si ses variables macroscopiques ne varient pas au cours du temps. Dans le cas contraire, il est hors d’équilibre. Un système, initialement hors d’équilibre, évolue de manière à atteindre l’équilibre. Ce dernier sera atteint au bout d’une durée appelé durée de relaxation.
La thermodynamique ne s’intéresse qu’aux systèmes en équilibre, contrairement à ce que le terme « dynamique » pourrait laisser penser. Dans la pratique, on ne peut pas observer un système sur une durée infinie, mais on se trouve assez souvent dans une situation où l’on étudie un système pendant une période très supérieure à sa durée de relaxation : dans ce cas, on peut le considérer comme étant à l’équilibre. Cet équilibre est alors associé à une configuration correspondant à une contrainte sur les variables macroscopiques qui n’ont pas encore atteint leur état d’équilibre. En effet, on peut associer une durée de relaxation à chaque variable macroscopique, et définir ainsi des systèmes ayant des contraintes sur certaines de ces variables et pour lesquels il existe un état d’équilibre.
Exemple : considérons de l’air enfermé dans une enceinte diatherme ayant la forme d’un cylindre dont l’une des bases est un piston mobile. Le milieu extérieur est supposé être à la température To et à la pression Po . L’état d’équilibre du système correspond à la configuration où la pression et la température du gaz sont égales à Po et To respectivement ; le volume sera alors égal à Vo .
Préparons initialement le système de manière à ce que le volume soit Vo / 2 est bloquons le piston dans cette position. Le système va très vite atteindre un état d’équilibre où la pression et la température sont respectivement 2 Po et To. En procédant ainsi, nous imposons une contrainte sur un des paramètres macroscopiques, en l’occurrence le volume. Pour chaque valeur de la contrainte, il existe un état d’équilibre thermodynamique différent. Si nous libérons le piston, i.e. si nous supprimons la contrainte sur le volume, le système n’est plus dans un état d’équilibre : il va évoluer de manière à atteindre l’état d’équilibre sans contrainte que nous avons évoqué plus haut. Au cours de cette évolution, le système échange du travail et de la chaleur avec le milieu extérieur.
Supposons à présent que le piston ne puisse se déplacer qu’à très faible vitesse et que la durée nécessaire pour passer de la configuration correspondant à Vo/2 à celle correspondant à Vo (équilibre final) soit très longue comparée à la durée nécessaire pour effectuer des échanges thermiques avec l’extérieur. Dans ce cas, on peut dire qu’à chaque instant le système sera en équilibre thermodynamique dans une configuration correspondant à une contrainte sur le volume V, qui évoluera entre Vo/2 et Vo . Si, au cours de cette évolution, on observe le système pendant un temps suffisamment court pour que le piston se déplace à peine, mais suffisamment long pour qu'il y ait équilibre thermique à chaque instant, tout se passe comme si nous avions affaire à un état d'équilibre du système avec contrainte sur le volume.
Nous avions déjà rapporté l'existence deux formes de transfert d'énergie : le travail et la chaleur. Sans trop anticiper, on peut faire les remarques suivantes :
le travail mécanique est un transfert d'énergie à l'échelle macroscopique. Si l'interaction de deux systèmes se traduit par un changement des paramètres macroscopiques autres que la température, on dit qu'il y a échange d'une quantité de travail W. Ainsi, le travail est d'origine mécanique si le paramètre macroscopique qui varie est le volume. Pour qu'il n'y ait qu'un échange de travail entre deux systèmes, il faut qu'ils soient séparés par une paroi adiabatique qui prévient tout échange de chaleur.
un échange de chaleur est un transfert d'énergie à l'échelle microscopique. Si l'interaction entre deux système se traduit par un changement de température à l'exclusion de tout changement des autres variables macroscopiques, on dit qu'il y a échange d'une quantité de chaleur Q. Cet échange cesse lorsque l'on a atteint l'équilibre thermique, et les températures sont alors égales. L'unité de travail ou de chaleur est le joule (J) ; pour les échanges de chaleur, on utilise parfois la calorie (cal), qui est la quantité de chaleur nécessaire pour augmenter la température d'un gramme d'eau sous une atmosphère de 14,5 à 15,5°C (soit : 1 cal = 4,18 J). Pour maintenir constante la température d'un système, on a souvent recours à un thermostat : c'est un réservoir de chaleur suffisamment grand pour que tout échange de chaleur avec le système considéré ne change pratiquement pas sa température.
Un système est homogène si, en l'absence de champ extérieur, la
concentration de ses constituants est la même en tout point. Dans le cas
contraire, il est dit hétérogène : c'est le cas, par exemple, d'un
mélange de pierres et d'eau. On peut toujours séparer un système hétérogène en
plusieurs systèmes homogènes dont on peut étudier les propriétés et les
interactions.
Si un système homogène est placé dans un champ extérieur, comme le champ de
pesanteur par exemple, la concentration de ses constituants peut varier d'un
point à un autre mais reste une fonction continue de la position.
On sait ainsi que la densité de l'air diminue lorsque l'altitude augmente.
Pour caractériser un système homogène composé de r constituants, contenus dans un volume V, il faut connaître le nombre de moles respectives de chacun d'eux : n1, n2, n3, ..., nr . Considérons deux système identiques et supposons qu'on les réunisse pour qu'ils n'en forment plus qu'un. Le volume de ce nouveau système sera 2 V et les nombres de moles de chaque espèce seront 2 n1, 2 n2, ..., 2 nr .
Toute quantité thermodynamique dont la valeur reste inchangée après cette
opération est qualifiée de grandeur intensive.
Si sa valeur est multipliée par deux, c'est une grandeur extensive.
Pour un système à un constituant, une variable intensive ne dépend pas de la masse de celui-ci, alors qu'elle lui est proportionnelle si cette variable est extensive. La pression et la température sont deux variables intensives alors que le volume et l'énergie sont des quantités extensives.
2 - Principes de la thermodynamique
Quatre propositions, admises a priori, constituent la base de la thermodynamique : ce sont les principes de la thermodynamique. Le bien fondé de leur choix est vérifié a posteriori par l'exactitude de leurs conséquences.
2.1 - Principe zéro
Si deux systèmes sont en équilibre thermodynamique avec un même troisième, ils sont en équilibre entre eux.
Ce principe est bien entendu évident pour notre sens commun. Considérons par exemple deux systèmes, 1 et 2, en équilibre thermique. Si nous mesurons la température du système I à l'aide d'un thermomètre, qui constitue le système 3, et si nous trouvons la valeur T, la température du système 2 sera bien évidemment elle aussi égale à T.
2.2 - Premier principe
On admet en Physique, et cela se vérifie par l'expérience, le principe très
général de la conservation de l'énergie totale d'un système isolé. La
restriction de cette hypothèse à la thermodynamique en constitue le premier
principe. Avant de l'énoncer, il est nécessaire d'apporter un certain nombre de
précisions.
L'énergie totale d'un système mécanique conservatif est égale à la somme de
l'énergie cinétique et de l'énergie potentielle des particules qui le
constituent (cette dernière peut résulter de l'interaction mutuelle de plusieurs
particules). Lorsque le système est isolé, et qu'il n'est soumis à aucune force
extérieure (ie. isolé au sens mécanique), son énergie totale reste constante au
cours de son évolution.
En thermodynamique, on appelle cette énergie totale l'énergie interne du système ; on l'écrira E. Si le système considéré n'est plus isolé, mais s'il interagit avec le milieu extérieur, son énergie interne va varier d'une quantité DE. Dans ce cas, le système change avec le milieu extérieur des quantités de travail W et de chaleur Q. Par convention, ces quantités sont comptées positivement si elles sont fournies par le milieu extérieur.
On traduit le premier principe de la thermodynamique par
DE = W + Q
Il exprime la conservation de l'énergie totale du système.
La quantité DE ne dépend que de l'état initial et de l'état final du système : l'énergie interne E est ce qu'on appelle une fonction d'état. Pour une transformation infinitésimale, le premier principe s'écrit
dE = dW + dQ
où dE est une différentielle totale. Mathématiquement, cela signifie que l'intégrale de la quantité dE d'un état initial i à un état final f ne dépend pas du chemin C suivi
![]()
Par contre, il est important de noter que ni le travail W ni la chaleur Q ne sont des fonctions d'état. L'échange de travail W, ou de chaleur Q, dépend du chemin suivi par le système au cours de son évolution. Pour cette raison, on note les variations infinitésimales de W et de Q par dW et dQ, respectivement, et non à l'aide de "d droits", comme pour l'énergie. Si l'une des quantités W ou Q est nulle au cours de la transformation, alors W (ou Q) est égale à DE et ne dépend que des états initial et final. Par exemple, une transformation adiabatique se fait sans échange de chaleur et Q = 0. Il s'ensuit alors W = DE.
Remarques
En thermodynamique, on suppose implicitement que l'énergie interne est une variable extensive. Cela signifie que, si l'on forme un seul système à partir de deux systèmes initialement identiques 1 et 2, l'énergie interne du système 1+2 est égale à
E1+2 = E1 + E2
Ceci n'est qu'une approximation, mais elle s'avère excellente pour les systèmes macroscopiques pour lesquels on applique les lois de la thermodynamique. En effet, nous avons en toute rigueur
E1+2 = E1 + E2 + E12
où E12 est l'énergie d'interaction entre les systèmes 1 et 2. Pour les systèmes macroscopiques en faible interaction, E12 est négligeable devant E1 et E2 et l'énergie interne peut être considérée comme une variable extensive. De manière plus précise, E est une variable extensive dans la limite dite thermodynamique où le nombre N de particules, et le volume V, tendent vers l'infini, leur rapport restant constant. La limite thermodynamique correspond à la situation où les effets de surface sont négligeables comparés aux effets de volume.
L'énergie interne doit être évaluée dans le référentiel du centre de masse associé à l'ensemble des particules constituant le système. C'est pour cette raison que l'on utilise le qualificatif interne pour désigner cette énergie. Si le système est animé d'un mouvement de translation ou de rotation d'ensemble, l'énergie associée à ce déplacement ne doit pas être comptabilisée dans l'énergie interne.
2.3 - Encore un peu de vocabulaire
La thermodynamique ne s'intéresse pas qu'aux états d'équilibre statique d'un système constitué d'un grand nombre de particules. Néanmoins, on l'utilise souvent pour étudier les propriétés initiales et finales d'un système en évolution. Ceci conduit souvent à considérer trois types de transformations qui jouent un rôle important dans ce contexte : les transformations quasi-statiques, réversibles et irréversibles.
La distinction entre énergie mécanique et chaleur conduit à appeler paramètres externes les variables thermodynamiques autres que la température (le volume, la pression, ...) ; la variation de ces paramètres externes peut créer du travail (par exemple lors d'une variation de volume). A chaque configuration des paramètres externes correspond un état d'équilibre thermodynamique.
Considérons un système dans une configuration initiale donnée et effectuons une transformation sur celui-ci en faisant varier certains paramètres externes.
Si son évolution est telle qu'il reste toujours en équilibre thermodynamique - caractérisé par la valeurs que prennent les paramètres externes au cours de la transformation - , la transformation est dite quasi-statique.
Si, de plus, par une simple inversion de la transformation, on peut retrouver l'état initial, elle est réversible.
Dans les deux cas il faut que les paramètres externes varient suffisamment lentement par rapport à la durée de relaxation du système.
Une transformation qui n'est pas réversible est dite irréversible.
Remarque : une transformation réversible est quasi-statique, mais une transformation quasi-statique n'est pas systématiquement réversible.
Exemple : Pour fixer les idées, considérons un gaz enfermé dans un cylindre aux parois adiabatiques dont l'une des bases est un piston mobile se déplaçant sans frottement. Lorsque le piston se déplace, on change le volume du cylindre (ie. un de ses paramètres externes). A chaque position du piston correspond un état d'équilibre. Si, lorsqu'on déplace le piston d'une distance Dx, la durée de relaxation est de l'ordre de la milliseconde, il suffit alors de le déplacer en quelques dixièmes de seconde pour que le processus soit considéré comme quasi-statique avec une excellente approximation.
Dans cet exemple, on peut calculer le travail effectué par le milieu extérieur sur le piston lorsque celui-ci se déplace, lentement, d'une distance dx vers l'extérieur (en considérant dx > 0). Si le système est en équilibre, la pression P est la même de chaque côté du piston ; la force qui agit des deux côtés du piston de surface S s'écrit alors F = P S , et on en déduit le travail effectué par le gaz vaut alors P S dx ; le travail effectué par le milieu extérieur est égal à
dW = - P S dx
ce qui s'écrit également, en considérant que S dx est aussi la variation dV du volume du gaz,
dW = - P dV
qui n'est évidemment valable que pour une transformation quasi-statique (équilibre à chaque instant).
Nous venons de voir qu'il est possible d'échanger du travail de manière quasi-statique avec le milieu extérieur. On peut aussi échanger de la chaleur de manière quasi-statique. Pour cela, on met le système en contact avec des thermostats successifs dont la température diffère très peu de celle du système au cours de son évolution.
2.4 - Deuxième principe : Damoclès ou la flèche du temps
Détrônons un peu la sacro-sainte conservation de l'énergie : si le premier principe contrôle le bilan d'énergie d'une transformation, il ne dit pas si celle-ci est possible.
Eh oui, dans la vie courante, nous savons que certaines transformations sont possibles alors que d'autres, tout en satisfaisant au premier principe, ne le sont pas : par exemple, si nous mettons une pièce de métal chaud dans un récipient d'eau froide, nous savons que la pièce de métal se refroidit et que l'eau s'échauffe ; il ne nous viendrait pas à l'esprit d'imaginer que la pièce métallique puisse devenir plus chaude et l'eau plus froide. Pourtant une telle réaction ne contredit en rien le premier principe du moment que l'énergie est conservée.
L'expérience quotidienne nous montre que la chaleur passe toujours d'un corps chaud vers un corps froid. Les transferts de chaleur ne se font que dans certaines directions et le second principe se pose en objet de dire lesquelles. Il existe plusieurs énoncés du second principe, qui s'attachent à décrire certains aspects différents des transferts de chaleur. Nous allons très brièvement les rappeler.
Enoncé de Clausius
Il n'existe pas de processus dont le seul résultat soit de transférer de la chaleur d'un corps froid vers un corps chaud.
Il est possible de faire passer de la chaleur d'un corps froid vers un corps chaud, mais il faut fournir un travail (c'est le principe du réfrigérateur par exemple). Par conséquent, si la chaleur passe d'un corps A à un corps B par conduction thermique, il n'existe pas de transformation dont le seul résultat soit de transférer de la chaleur du corps B vers le corps A.
Enoncé de Kelvin-Planck
Il n'existe pas de transformation dont le seul résultat soit de produire du travail à partir d'une seule source de chaleur à température constante.
Cela signifie qu'il faut au moins deux sources à des températures différentes pour réaliser une conversion d'énergie calorifique en énergie mécanique. Les cycles de Carnot, qui sont une suite cyclique de transformations quasi-statiques utilisant deux sources de chaleur aux températures T1 et T2 (en supposant, par exemple, T1 > T2), jouent un rôle particulièrement important dans le problème de la transformation de chaleur en travail.
Voyons ceci de plus près en utilisant l'exemple du gaz contenu dans un cylindre dont la base est un piston mobile sans friction. Nous allons soumettre ce gaz à une suite de transformations quasi-statiques produisant un cycle de Carnot que l'on peut représenter dans un plan (P,V).
Description du cycle de Carnot
Initialement, nous partons du point A où le gaz est à la pression P1 et à la température T1. Il occupe alors un volume V1. Le système est mis en contact avec un thermostat à la température T1 (dite source chaude) et on lui fait subir une transformation isotherme (température constante) réversible jusqu'à la pression P2 en variant de manière quasi-statique la pression exercée sur le piston mobile : le gaz est détendu. Dans le plan (P,V), le système décrit l'arc AB et le volume final est V2 > V1. Pour maintenir constante sa température, le gaz a reçu une quantité de chaleur Q1 > 0 de la source chaude car nous savons qu'un gaz en expansion a tendance a se refroidir.
Le système est alors isolé par une paroi adiabatique, ce qui prévient tout échange de chaleur avec l'extérieur. On effectue une détente adiabatique réversible de manière à ce que la température soit égale à T2, la température de la source froide. Le système décrit alors l'arc BC.
Le système est mis en contact avec la source froide, qui va jouer le rôle d'un thermostat à la température T2, et on effectue une compression isotherme quasi-statique jusqu'au point D (situé sur l'adiabatique passant par A) ; au cours de cette transformation, le système reçoit la quantité de chaleur Q2 < 0 car la compression d'un gaz tend à le réchauffer.
On ferme le cycle par une compression adiabatique réversible qui fait passer le système du point D au point A, de même que sa température de la valeur T2 à la valeur T1.
Bilan énergétique
Comme nous avons effectué un cycle, la variation d'énergie interne DE est nulle. Le transfert de chaleur vaut Q = Q1 + Q2 avec Q1 > 0 et Q2 < 0.
Le travail échangé entre le système et le milieu extérieur dans la transformation ABC est égale à W1 ; cette quantité est négative (le système fournit du travail au milieu extérieur) et est égale à l'aire comprise entre l'axe des abscisses et la courbe ABC.
Le travail échangé dans la transformation CDA est égal à W2 > 0.
Au cours de ce cycle, le gaz a échangé une quantité de travail W = W1 + W2 < 0 qui est égale à l'aire du cycle. Le système a donc globalement fourni du travail au milieu extérieur. Afin de traiter des grandeurs positives, nous poserons W1' = -W1 et
Q2' = -Q2. Ces deux grandeurs sont respectivement le travail et la chaleur fournis au milieu extérieur lors des transformations ABC et CDA.
Le premier principe conduit à
DE = W + Q = W1 + W2 + Q1 + Q2 = 0
soit
W1' - W2 = Q1 - Q2'
On définit le rendement h du cycle comme le rapport entre la quantité de travail fournie par le système et la quantité de chaleur prise à la source chaude :
![]()
On trouve à travers le cycle de Carnot une définition de l'échelle absolue de température,
![]()
ce qui permet d'écrire le rendement sous la forme
![]()
Tous les cycles quasi-statiques fonctionnant entre T1 et T2 ont le même rendement ; en revanche, les cycles contenant des transformations irréversibles ont un rendement inférieur. Les cycles quasi-statiques correspondent au cas où le travail fourni est maximal. Pourtant, les rendements sont peu élevés : si T1 = 400 K et T2 = 300 K, le rendement n'est que de l'ordre de 25%.
Remarque : un cycle de Carnot qui fonctionnerait en sens inverse du précédent décrirait un système se comportant comme un réfrigérateur.
Introduction naturelle de l'entropie
En revenant aux quantités définies selon les conventions de signe de la thermodynamique, l'équation peut être écrite sous forme
![]()
et peut être généralisée à tout cycle quasi-statique sous la forme
![]()
où l'intégrale est prise le long du cycle et dQq-s représente la quantité de chaleur échangée de manière quasi-statique avec le système au point du cycle où la température vaut T. L'équation précédente constitue le théorème de Clausius ; il permet d'introduire une quantité fondamentale en thermodynamique, l'entropie S, définie par
![]()
Ainsi, ici,
![]()
L'entropie est donc une fonction d'état et, par suite, la différence d'entropie entre deux états thermodynamiques ne dépend pas du chemin suivi, mais seulement des états initial et final. Il est important de noter que, par contre, dQq-s n'est pas une fonction d'état. La température T est en fait le facteur intégrant qui permet de transformer dQq-s en différentielle totale dS.
Tout comme l'énergie interne, l'entropie est une variable extensive dans la limite thermodynamique. Elle permet une autre formulation importante du second principe de la thermodynamique : l'entropie d'un système isolé ne peut qu'augmenter. Rappelons pour mémoire qu'un processus est réversible si DS = 0 et qu'il est irréversible si DS > 0.
Exemple
Considérons un système dans un état d'équilibre A et faisons lui subir une transformation qui l'amènera dans un état d'équilibre B. Pour ce faire, il faut que le système interagisse avec le milieu extérieur. En effet, s'il était isolé et en équilibre, il n'évoluerait pas. Soit DSs la variation d'entropie du système et DSe celle du milieu extérieur. L'ensemble {système + milieu extérieur} forme un système fermé auquel nous pouvons appliquer le second principe. Dans ce cas, DSs + DSe = 0 si la transformation est réversible, et DSs + DSe > 0 si elle est irréversible. Dans cette dernière situation, le système produit plus d'entropie que le milieu extérieur n'en absorbe et au total l'entropie de l'univers (ensemble total) augmente.
Exemple
Considérons deux systèmes, l'un à la température T1 = 350 K et l'autre à T2 = 300 K. Mettons les brièvement en contact thermique par l'intermédiaire d'une paroi diatherme et supposons qu'un joule soit transféré du premier vers le second système, de manière quasi-statique, sans que la température de ceux-ci ne soit modifiée (ils sont supposés avoir une grande capacité calorifique). Voyons si cette transformation est possible. L'ensemble des deux systèmes est fermé. Sa variation d'entropie DS vaut DS = DS1 + DS2 où DS1 et DS2 sont les variations d'entropie de chacun des systèmes. Nous avons
![]()
L'entropie du système total a augmenté, ce qui est en accord avec le second principe. Par contre, la transformation dans laquelle un joule serait passé du second au premier système est impossible, car l'entropie du système total devrait alors diminuer.
Le second principe de la thermodynamique dit que l'entropie de l'univers augmente dès qu'un processus irréversible a lieu. Nous verrons par la suite que l'entropie est liée au désordre du système. La loi d'accroissement de l'entropie indique que l'évolution d'un système fermé ne peut se produire que vers des états qui sont de plus en plus désordonnés au niveau microscopique. Pour cette raison, on dit souvent en biologie que lorsque l'entropie augmente l'énergie se "dégrade" car elle se répartit sur un plus grand nombre de degrés de liberté.
Question paradoxale : et le mécanisme de solidification ou de condensation, alors ?
Réversibilité et irréversibilité : quelques précisions
Nous disposons à présent de tous les éléments pour définir précisément la notion de transformation irréversible, réversible et quasi-statique.
L'état d'un système isolé en équilibre thermodynamique est complètement déterminé si on connaît son énergie E, son volume V et le nombre de particules Ni de type i dont il est constitué (nous supposerons qu'il y a r types de particules différents). Son entropie est une fonction de ces variables macroscopiques : S = S(E,V,N1,...,Nr).
Appelons {X} l'ensemble des variables (E,V,N1,...,Nr). On peut construire un espace à (r + 3) dimensions dans lequel un point de coordonnées (S,E,V,N1,...,Nr) correspond à une configuration particulière du système en équilibre thermodynamique. Un tel espace est représenté de manière schématique sur la figure suivante, sous forme d'un plan dont l'un des axes est S et l'autre {X} - ce dernier regroupe toutes les dimensions E, V, N1, ..., Nr.
Une trajectoire dans cet espace correspond à une transformation quasi-statique car c'est une suite d'états d'équilibre thermodynamiques. Si celle-ci se fait à entropie constante (transformation AB sur la figure), elle est réversible. Dans le cas contraire, elle est irréversible (transformation CD par exemple). Dans cette dernière situation, la transformation d'un système isolé ne peut se faire que par augmentation de l'entropie (en vertu du second principe). Une transformation réversible est toujours quasi-statique, mais l'inverse n'est pas vrai.
De même qu'il existe des transformations quasi-statiques qui ne sont pas réversibles, il existe des transformations irréversibles qui ne sont pas quasi-statiques. Etudions par exemple une transformation où les états initial et final sont des états d'équilibre. Si la transformation est irréversible et quasi-statique, elle se fait par une succession d'états d'équilibre et peut être décrite par une trajectoire dans l'espace constitué par les paramètre S et {X}.
Si la transformation est irréversible mais non quasi-statique, elle passe par une succession d'états qui n'appartiennent pas forcément à l'espace (S,{X}) car ce ne sont pas des états d'équilibre. Pour les décrire, il faut introduire des paramètres additionnels {Y} qui dépendent de la nature de la transformation. Le système va donc évoluer dans l'espace (S,{X},{Y}) de dimension plus grande que l'espace (S,{X}) associé aux états d'équilibre. Dans la figure suivante, on essaie de représenter très schématiquement ceci dans un espace à 3 dimensions.
Nous supposons que le sous-espace (S,{X}) associé aux configurations d'équilibre était le plan correspondant à {Y} = 0 même si la surface peut être beaucoup plus compliquée que cela. La transformations AB est irréversible (S augmente) mais quasi-statique. Elle reste toujours dans le sous-espace (S,{X}) des états d'équilibre thermodynamique.
La transformation CD est irréversible et non quasi-statiques car, si C et D sont supposés appartenir au plan (S,{X}), tous ses points n'appartiennent pas à ce plan. Au début, elle sort du plan vers les {Y} positifs, le retraverse pour aller vers les {Y} négatifs.
Pour un système isolé, toute transformation se fait avec DS > 0. Cela ne veut pas dire qu'il n'est pas possible de diminuer l'entropie du système, mais une telle diminution ne peut être obtenue que par un échange d'énergie avec le milieu extérieur, si bien que le système étudié n'est plus isolé. Au passage, voici la réponse à notre question "paradoxale" pour la solidification ou la condensation...
2.5 - Troisième principe
Si on intègre l'équation
![]()
entre T = 0 et une température quelconque, il apparaît systématiquement une constante arbitraire So. Aucun des principes thermodynamiques introduits jusqu'à présent ne permet de déterminer la valeur de cette constante So. Cela n'a en général pas grande importance car, dans la pratique, on a toujours à calculer une différence entre les valeurs de S associées à deux macroétats. Par suite, la constante s'élimine. Il est néanmoins intéressant de pouvoir déterminer S de manière absolue et pas seulement à une constante près. C'est l'objet du troisième principe, proposé par Nernst en 1906 :
L'entropie d'un solide ou d'un liquide pur en équilibre thermodynamique est nulle au zéro absolu.
Ce principe apparaît naturellement dans le cadre de la Physique statistique, comme nous le verrons.
3 - Fonctions thermodynamiques
3.1 - Introduction du formalisme énergétique
Soit un système homogène de r constituants ayant N1, N2, ..., Nr particules de type 1, 2, ..., r. L'énergie interne E est une fonction des paramètres extensifs S, V, N1, N2, ..., Nr.
E = E(S,V, N1, N2, ..., Nr)
A chaque paramètre extensif correspond un paramètre intensif qui est, sauf pour la pression, égal à la dérivée partielle de E par rapport à ce paramètre, les autres paramètres restant constants. Dans le cas de la pression, on rajoute un signe moins (variation inverse avec le volume : plus le volume diminue, plus la pression augmente).
Le paramètre intensif associé à l'entropie S est la température T
![]()
Le paramètre intensif associé au volume V est la pression P
![]()
Le paramètre intensif associé au nombre Nj de particules de type j est le potentiel chimique µj
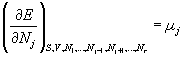
La différentielle de l'énergie est totale (fonction d'état) et s'écrit
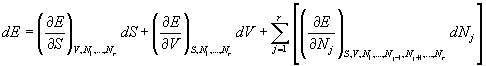
et, compte tenu des définitions précédentes, il vient
![]()
Cette expression est très fréquemment rencontrée en thermodynamique. Ici, on a supposé que le nombre de particules de chaque type pouvait varier, ce qui induit bien évidemment des changements dans l'énergie interne. Pour un système homogène à un constituant, dont le nombre de particules ne varie pas, on obtient simplement
dE = T dS - P dV
Cette relation n'est valable que pour les transformations quasi-statiques, et vaut également
dE = T dS - P dV = dQ + dW
Comme l'énergie interne est une fonction extensive, on peut calculer son expression en fonction de S, V et N (en se limitant à un seul constituant pour alléger les notations, même si la généralisation à plusieurs constituants est immédiate). En effet, une grandeur extensive est une fonction homogène du premier ordre. Si l est un paramètre quelconque, cette propriété s'exprime par la relation
E(lS,lV,lN) = l E(S,V,N)
En dérivant par rapport à l, on obtient
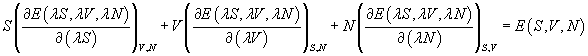
Cette équation restant valable pour toute valeur du paramètre l, en particulier pour l = 1, il vient :
![]()
En introduisant les paramètres intensifs T, P et µ, il vient
E = T S - P V + µ N
qui est la forme d'Euler de l'énergie interne.
Si on connaît l'expression E = E(S,V,N1,...,Nr), on peut calculer l'état d'équilibre thermodynamique d'un système correspondant éventuellement à des contraintes sur certains des paramètres externes (V, N1, ..., Nr). Si, comme c'est le cas pour un système isolé, l'énergie interne E est fixée, cet état d'équilibre est obtenu lorsque S est maximum (s'il y a des contraintes sur certains paramètres externes, on doit en tenir compte lors de la recherche de ce maximum). Si au contraire S est fixée, l'équilibre thermodynamique est atteint lorsque E est minimum. Il est souvent facile d'imposer une contrainte sur le volume d'un système macroscopique ; il est par contre difficile de fixer l'entropie de celui-ci à une valeur déterminée. Par contre, il est facile de fixer la température d'un système en le mettant en contact avec un thermostat, ou de lui imposer une pression déterminée. Beaucoup d'expériences ont ainsi lieu à température et/ou pression constante. Lorsque c'est le cas, il est beaucoup plus commode d'utiliser d'autres fonctions d'état que l'énergie pour étudier la thermodynamique du système en fonction des contraintes sur les paramètres externes qui sont données. Ces fonctions thermodynamiques s'obtiennent le plus souvent à partir de l'énergie interne après une transformation appropriée appelée transformation de Legendre.
3.2 - Transformation de Legendre et obtention de nouvelles fonctions thermodynamiques
On appelle transformation de Legendre une opération permettant de changement l'ensemble des variables descriptives soit, par là même, de changer de fonction thermodynamique.
L'énergie interne se met sous la forme différentielle générale
dE = dQ + dW = T dS + Y dX
où Y(intensive) et X(extensive) sont deux variables conjuguées par rapport à l'énergie (cf. 3.1)
En retranchant ou en ajoutant à l'énergie interne les produits de la variable X par la variable énergétique associée Y, on obtient une nouvelle fonction thermodynamique
f = U(S,V) - XY
dont la différentielle s'écrit
df = T dS + Y dX - d(XY) = T dS - X dY
Nous fabriquerons ainsi l'enthalpie H.
En procédant de la même manière pour l'entropie S, on obtient la fonction dite "libre" en retranchant la quantité TS
f' = U(S,V) - XY - TS
dont la différentielle s'écrit
df' = T dS + Y dX - d(XY) - d(TS) = - S dT - X dY
Nous fabriquerons l'énergie libre F et l'enthalpie libre G de cette façon.
3.2 - La fonction enthalpie H
Négligeons tout d'abord le potentiel chimique. Lorsque la pression est constante, le travail élémentaire des forces de pression n'est pas nul est vaut -P dV où P = Cte. Le bilan énergétique s'écrit, pour le système,
dE = dQ + dW = dQ - P dV = dQ - d(PV)
soit
dQ = d(E + PV)
et il est commode d'introduire une nouvelle fonction d'état, l'enthalpie H, telle que
H = E + PV
La différentielle de cette fonction s'écrit
dH = dE + d(PV) = dQ + dW + P dV + V dP = T dS - P dV + P dV + V dP
soit
dH = T dS + V dP
H apparaît bien comme une fonction thermodynamique associée aux variables S et P.
Nous avons également les relations
![]()
![]()
et la relation de Maxwell relative à l'enthalpie (théorème de Schwarz)
![]()
La transformation de Legendre qui a conduit à l'enthalpie H depuis l'énergie interne E consiste à ajouter la quantité PV à cette dernière. Elle s'écrit, de manière générale,
![]()
3.3 - La fonction énergie libre F
La fonction énergie libre ou fonction de Helmholtz F (de l'anglais free) s'obtient en retranchant la quantité TS à l'énergie interne E
F = E - TS
La différentielle de cette fonction s'écrit
dF = d(E - TS) = dQ + dW - d(TS) = T dS - P dV - T dS - S dT
soit
dF = -P dV - S dT
On en tire les équations suivantes :
![]()
![]()
et l'équation de Maxwell relative à l'énergie libre
![]()
L'énergie libre est utilisée lors d'expériences à température constante. De façon générale, elle s'écrit
![]()
Pour les systèmes en contact avec un thermostat dont la température est T, l'équilibre thermodynamique est atteint en minimisant l'énergie libre F.
3.4 - La fonction enthalpie libre G
La fonction enthalpie libre ou fonction de Gibbs G s'obtient en retranchant la quantité TS à l'enthalpie H,
G = H - TS
Sa différentielle s'écrit
dG = d(H - TS)
= d(E + PV) - S dT - T dS
= dQ + dW + P dV + V dP - S dT - T dS
= T dS - P dV + P dV + V dP - S dT - T dS
soit
dG = - S dT + V dP
On en tire les équations
![]()
![]()
et la relation de Maxwell relative à l'enthalpie libre
![]()
L'enthalpie libre G est très utile en Chimie, où l'on travaille souvent à température et pression constante. Elle s'écrit généralement
![]()
A pression et température constantes, l'équilibre thermodynamique est assuré lorsque G est minimum.
3.5 - La fonction grand potentiel Ψ
Lorsqu'on s'intéresse aux gaz parfaits de Bose ou de Fermi, comme nous le verrons, il est souvent utile de choisir les variables T, V et µ1, ..., µr. Pour un constituant par exemple, ceci conduit à définir le grand potentiel Ψ en retranchant à l'énergie libre la quantité µN
Ψ = F - µN
La différentielle s'écrit
dΨ = d(F - µN)
= d(E - TS) - d(µN)
= T dS - P dV - S dT - T dS - N dµ
soit
dΨ = - S dT - P dV - N dµ
En complément : les coefficients calorimétriques
Pour le couple de variables (T,V), on peut écrire
![]()
avec
![]()
![]()
Pour le couple de variables (T,P), on a de même
![]()
avec
![]()
![]()
Les coefficients CV et CP sont les capacités thermiques à volume constant et à pression constante ; ils représentent la chaleur nécessaire pour faire varier la température du système de 1 K, de façon réversible, les autres variables V ou P étant maintenues constantes.
Les coefficients l et k sont appelés chaleurs latentes : ce sont les chaleurs nécessaires pour provoquer, de façon isotherme et réversible, des variations de volume ou de pression égales à l'unité.
On peut ensuite donner l'expression de l'énergie interne et de l'enthalpie en fonction des coefficients précédents.
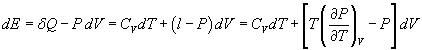
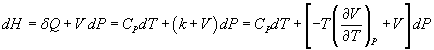
Par conséquent,
|
|
|
| et | |
|
|
|
Les relations de Maxwell
|
|
|
permettent d'en déduire les relations de Clapeyron
![]()
![]()
Ces équations permettent, connaissant par exemple l'équation d'état d'un fluide, de déterminer les expressions de l et de k. Pour le gaz parfait, notamment, on peut en tirer les lois de Joule qui indiquent que l'énergie interne et l'enthalpie d'un gaz parfait ne dépendent que de la température.