Le monde microscopique

La Physique Statistique permet de faire le lien entre les mondes macroscopiques et microscopiques. A notre échelle, on peut définir une configuration particulière d'un système macroscopique (macroétat) en se donnant la valeur de toutes ses variables thermodynamiques indépendantes. Par exemple, pour un gaz parfait, il suffit de fixer trois paramètres choisis par la pression, le volume, la température et le nombre de particules du gaz. Le quatrième paramètre est alors obtenu à partir de l'équation d'état des gaz parfaits. Peu de paramètres sont donc nécessaires pour déterminer un macroétat, i.e. la configuration d'un système à notre échelle.

Un corps macroscopique est constitué d'un nombre extrêmement grand de composants élémentaires ou particules : atomes, molécules, électrons, nucléons, ... Si l'on étudie le système au niveau de ses constituants, on s'intéresse au monde microscopique. Il convient à ce stade d'analyser les caractéristiques principales des constituants élémentaires de ce corps tels que nous venons de les citer,

• ils sont extrêmement petits : cela signifie que leurs propriétés sont souvent dominées par les phénomènes quantiques.

• ils sont extrêmement nombreux : leur évolution ne peut donc pas être traitée individuellement mais comme un élément particulier d'un ensemble aux propriétés plus globales : c'est l'objet d'une physique dite statistique.

Paradoxalement, il est plus facile d'introduire la physique statistique à partir de la mécanique quantique qu'à partir de la mécanique classique (newtonienne), bien que le formalisme soit plus rédhibitoire. Nous ferons abondamment appel aux propriétés quantiques des particules telles qu'elles sont décrites dans les introductions à la mécanique quantique. Mais la mécanique classique permettra, dans de nombreux cas - comme celui du gaz parfait dans les conditions ordinaires - une description plus simple mais tout aussi réaliste de l'évolution des constituants d'un système.

A un instant donné, les particules d'un système sont dans une configuration qu'on appelle micro-état. La définition de celui-ci permet de déterminer complètement le système au niveau microscopique. Il est important de noter qu'on ne peut pas, dans la pratique, déterminer le micro-état d'un système macroscopique. Pour une mole de gaz, par exemple, soit N_A = 6,02.10²³ particules, si nous utilisions la mécanique classique pour décrire l'évolution des molécules de gaz, il faudrait connaître 3 NA positions et 3 Na vitesses pour complètement déterminer le système : c'est une tâche impossible à réaliser pratiquement, d'autant que la connaissance d'une telle configuration serait de bien peu d'intérêt au niveau macroscopique.

1 - Micro-états quantiques

Illustrons les configurations microscopiques particulières d'un système à travers quelques exemples usuels.

    1.1 - L'atome d'hydrogène

Le constituant principal de la matière est aussi le plus simple. L'atome d'hydrogène est un système constitué d'un proton et d'un électron qui interagissent par l'intermédiaire d'une force électrique coulombienne attractive. Dans une image classique, les deux particules tournent autour du centre de masse du système ; comme le proton est 1 836 fois plus lourd que l'électron, on peut en première approximation considérer qu'il est immobile et que l'électron tourne autour de lui. Ce sont les caractéristiques de son mouvement, à lui et à lui seul, qui vont déterminer les propriétés chimiques de cet élément. Par conséquent, on est ramené à étudier le problème d'une particule : l'électron.

Dans cet exemple très simple, l'énergie potentielle de l'électron est de type coulombien. Comme elle est définie à une constante près, nous pouvons supposer qu'elle est nulle lorsque le proton et l'électron sont infiniment éloignés l'un de l'autre. Cette énergie potentielle devient de plus en plus négative (l'électron et le proton s'attirent de plus en plus) à mesure que les deux particules se rapprochent. L'énergie totale du système, E, est égale à la somme de l'énergie potentielle et de l'énergie cinétique. Deux cas peuvent alors se présenter,

• si E > 0, on a un état de diffusion comme on peut en observer lors de la collision entre un électron et un proton. L'énergie E peut varier de façon continue et prendre toutes les valeurs possibles entre zéro et l'infini.

• Si E < 0,  on a un état lié. L'électron et le proton restent toujours très proches et ne peuvent s'éloigner indéfiniment l'un de l'autre. Contrairement à ce que prévoit la mécanique classique, où E pourrait prendre n'importe quelle valeur négative, la mécanique quantique prédit - et cela est confirmé par l'expérience, notamment en spectroscopie - que seules certaines valeurs de E sont permises. Les états d'énergie sont quantifiés et ne peuvent prendre que les valeurs vérifiant

Dans cette expression, où 1 eV = 1,6.10^-19 C, n est un entier strictement positif appelé nombre quantique principal. L'état fondamental de l'atome d'hydrogène correspond à n = 1 et vaut e₁ = -13,6 eV. Les états d'énergie supérieure sont appelés états excités et correspondent à n > 1. Pour un état d'énergie donnée e_n, il existe plusieurs configurations possibles correspondant aux nombres quantiques l, m, s et s_z qui obéissent aux lois suivantes,

• 0 < l < n - 1 avec l un entier appelé nombre quantique secondaire ; il est lié au moment angulaire orbital de l'électron.

• -l < m < +l   avec m un entier appelé nombre quantique magnétique ; il est lié à la projection du moment angulaire orbital sur un axe Oz.

• s = 1/2 : ce nombre quantique, appelé nombre quantique de spin, correspond à un degré de liberté purement interne à l'électron. Il n'a pas d'équivalent classique même si on est tenté de lui associer l'image d'une rotation intrinsèque de la particule autour d'un axe de symétrie.

• -1/2 < s_z < +1/2 : c'est le saut quantique lié à la projection de spin sur l'axe Oz. Ce nombre ne peut varier que par sauts d'une unité ; ici, il ne peut prendre que deux valeurs, +1/2 ou -1/2.

Remarque : moments angulaires orbital et de spin se mesurent en J.s, une unité qui a la même dimension que celle de la constante de Planck, h = 6,62.10^-34 J.s ; en mécanique quantique, on montre que le moment angulaire est quantifié et vaut un nombre entier ou demi-entier d'unités ħ = h/2p. Lorsqu'on dit que le spin est +1/2, cela signifie que la mesure du spin est ħ/2.

Une configuration correspond à la donnée de l'ensemble des nombres quantiques (n,l,m,s,sz) qui permettent de décrire complètement le système au niveau microscopique : c'est un micro-état. Dans le cas où une même valeur de l'énergie correspond à plusieurs configurations, ou micro-états, on dit que le niveau est dégénéré. Le degré de dégénérescence est le nombre de configurations associées à ce niveau d'énergie. Par exemple, si n =1, la dégénérescence est égale à 2 (puisque seul le nombre s_z peut prendre deux valeurs, ±1/2). Si n = 2, vous pourrez vérifier que la dégénérescence est égale à huit... A l'état correspondant à n = 2, on peut donc associer 8 micro-états.

Remarque : on doit définir un micro-état par un ensemble complet de nombres quantiques correspondant à des observables qui peuvent être mesurées simultanément (on dit que les opérateurs associés à ces grandeurs commutent). Pour l'atome d'hydrogène, on peut choisir comme observable l'énergie, le carré du moment angulaire orbital L², sa projection L_z sur l'axe Oz, le carré du spin s² et sa projection s_z. Ce choix particulier conduit à introduire l'ensemble des nombres quantiques n, l, m, s et s_z.

L'existence de niveaux d'énergie n'est pas prévue par la mécanique classique. Par exemple, celle-ci autoriserait toutes les valeurs négatives de l'énergie. Mais elle prévoit qu'un électron en rotation rayonne : son énergie cinétique devrait donc diminuer, et il tomberait finalement sur le noyau, si bien que même dans son état fondamental, un tel atome devrait être instable - ce qui n'est pas le cas. La mécanique quantique prévoit, au contraire,  que l'atome d'hydrogène est stable dans son état fondamental et que les niveaux d'énergie sont quantifiés. On peut cependant avoir des transitions entre deux niveaux d'énergie par absorption ou émission d'un photon, ce qui conduit, par suite de la quantification des niveaux, à l'observation de raies dans les spectres. La mécanique quantique permet de calculer exactement la longueur d'onde associée à ces raies : on retrouve la loi de Ritz (1908) obtenue initialement de manière empirique. Le photon émis (ou absorbé) lors de la transition emporte (ou amène) une quantité d'énergie égale à la différence entre les valeurs de l'énergie des niveaux correspondants.

Contrairement à ce que prévoit la mécanique classique, il est impossible de localiser exactement l'électron dans l'espace. Seule la probabilité de le trouver en un point donné peut être déterminée. Cette probabilité est proportionnelle au carré de la fonction d'onde associée à l'électron. En mécanique classique, on décrirait l'électron par sa position et sa vitesse ; en mécanique quantique, on le décrit à l'aide de la fonction d'onde qui est caractérisée par la donnée d'un ensemble complet de nombres quantiques (n,l,m,s,s_z), et rappelons au passage que s et s_z sont associés à des propriétés purement quantiques de l'électron qui n'ont pas d'équivalent classique rigoureux. Les nombres n, l et m décrivent les propriétés de l'électron dans l'espace ordinaire Ils sont au nombre de trois et ce nombre correspond justement au nombre de degrés de liberté dans l'espace ordinaire où, en mécanique classique, ce problème se réduit à celui d'une particule fictive tournant autour du centre de masse de l'atome.

Remarque : la donnée d'un ensemble complet de nombres quantiques est nécessaire pour préciser exactement la configuration microscopique d'un système. En effet, si cet ensemble est incomplet, on ne définit pas un micro-état mais une famille de micro-états. L'analogie avec la mécanique classique permet de mieux comprendre ce point : pour déterminer complètement la configuration d'une particule, il faut connaître sa position (x,y,z) et sa vitesse (vx,vy,vz), soit 6 quantités ; la donnée de 5 quantités seulement, par exemple, laisse la position ou la vitesse de la particule indéterminée, ce qui correspond à une infinité de configurations différentes.

    1.2 - L'oscillateur harmonique à une dimension

L'évolution d'une masse suspendue à un ressort autour de sa position d'équilibre, après qu'il en ait été légèrement écarté, représente un exemple d 'oscillateur harmonique classique. Supposons que la masse m soit susceptible de se déplacer dans une seule direction, que nous noterons x. Nous supposerons que la position d'équilibre correspond à x = 0. Ce système a le comportement d'un oscillateur harmonique si son énergie potentielle U est de la forme

où K est une constante. Si tel est le cas, le corps de masse m est soumis à une force de rappel telle que

et l'équation du mouvement s'écrit

où t désigne le temps. La solution de cette équation est une fonction sinusoïdale du temps dont la pulsation w est donnée par

Le système oscille autour de sa position d'équilibre avec la pulsation w i.e. avec la fréquence f = w/2p. Classiquement, toutes les valeurs positives de l'énergie sont permises.

Au niveau microscopique, il existe également des systèmes dont l'énergie est une forme quadratique des coordonnées. Un exemple très simple est donné par la molécule de dihydrogène dont les deux atomes H peuvent osciller le long de l'axe de symétrie de la molécule. La description de tels systèmes requiert l'utilisation de la mécanique quantique et cette dernière prédit que les niveaux d'énergie - donc les pulsations - sont quantifiés. Dans le cas d'un oscillateur harmonique à une dimension, les niveaux d'énergie sont donnés par la relation

où n est un entier positif ou nul : c'est le nombre quantique associé à un oscillateur à une dimension. Les niveaux d'énergie sont représentés ci-dessous.

Les niveaux d'énergie ne sont pas dégénérés. L'état fondamental correspond à n = 0 et son énergie vaut e_o = ħw/2. L'oscillateur "oscille" même dans son état fondamental puisque son énergie totale (potentielle plus cinétique) n'est pas nulle. Ceci est différent de la mécanique classique où l'état d'énergie le plus bas correspond à une configuration où le ressort est au repos.

Le fait que l'énergie totale d'un oscillateur harmonique quantique ne puisse pas être nulle dans son état fondamental peut être compris à l'aide du principe d'incertitude de Heisenberg, selon lequel il n'est pas possible de mesurer simultanément la position x et l'impulsion p_x d'une particule. En effet, on doit toujours avoir l'inégalité

où Dx et Dp_x sont respectivement les largeurs des distributions de probabilité en x et en p_x. Comme la forme de l'énergie potentielle oblige le système à rester dans une portion finie de l'espace, on a Dx ≠ 0et positif. Il s'ensuit que

et le système est toujours en mouvement.

    1.3 - Particule libre dans une boîte cubique

L'exemple d'une particule libre, de masse m, de spin nul, placée dans une boîte cubique de côté L est très formateur. L'énergie potentielle de ce système est nulle à l'intérieur de la boîte et infiniment répulsive (U → + ∞) à l'extérieur de manière à confiner la particule à l'intérieur du cube. Comme dans les deux exemples précédents, l'énergie de la particule (purement cinétique dans ce cas) ne peut être quelconque : seules certaines valeurs sont permises par la mécanique quantique :

où n_x, n_y et n_z sont des entiers strictement positifs. Ce sont les nombres quantiques associés à chacune des directions de l'espace. Cette expression s'obtient en résolvant l'équation de Schrödinger associée à la fonction d'onde de la particule,

C'est une équation aux valeurs propres pour l'opérateur hamiltonien

qui est associé à l'énergie de la particule (D représentant l'opérateur laplacien). Le problème lié à la résolution de cette équation est connu en mathématiques sous le nom de problème de Sturm-Liouville. Le rôle du laplacien est central et permet de séparer les variables d'espace en posant

On obtient

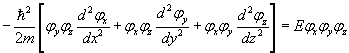
En divisant par la fonction et en multipliant par 2m/ħ², il vient

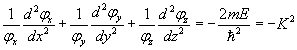
En écrivant la relation précédente sous la forme

on met en évidence le fait que le premier membre ne dépend que de x et que le second dépend de y et de z. Comme x, y et z sont des variables indépendantes, il ne peut y avoir égalité que si les deux membres sont égaux à une constante, que nous appellerons -K_x² :

en utilisant un raisonnement analogue sur le second membre, il vient

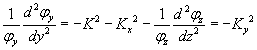
Au final, l'équation initial se réduit à trois équations différentielles identiques et simples,

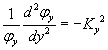où K_x² + K_y² + K_z² = K². La solution de la première équation a la même forme que celle d'un oscillateur harmonique,

Comme l'énergie potentielle est infinie à l'extérieur de la boîte, nous devons assurer j_x = 0 lorsque x < 0  et x > L. Ces conditions aux limites conduisent à A_x = 0 et K_xL = n_xp, où n_x est un nombre entier positif. Les équations relatives à j_y et j_z conduisent à des solutions identiques, donc

où C = B_xB_yB_z est une constante. Pour que |f|²dx dy dz représente la probabilité de présence de la particule dans l'élément de volume dx dy dz, il faut que f soit normalisée à l'unité, ce qui permettra de déterminer C :

ce qui donne

Les niveaux d'énergie sont quantifiés puisque K_x, K_y et K_z le sont :

d'où l'on tire

Posons par commodité

afin d'écrire

L'état fondamental correspond à n_x = n_y = n_z = 1 et son énergie vaut e₁₁₁ = 3 e_o. Il n'est pas dégénéré. Le premier état excité peut être construit de trois manières,

• n_x = 2, n_y = 1 et n_z = 1
• n_x = 1, n_y = 2 et n_z = 1
• n_x = 1, n_y = 1 et n_z = 2

Ces trois configurations, ou micro-états, conduisent en effet à la même valeur de l'énergie : e₁₁₂ = e₁₂₁ = e₁₁₂ = 6 e_o.

La dégénérescence du premier état excité est donc égale à trois. On peut, de la même manière, construire les états excités suivants en prenant garde de bien ordonner les niveaux d'énergie par ordre croissant. Cette tâche devient bien vite difficile dès que n_x, n_y et n_z prennent des valeurs appréciables. Enumérons, par exemple, le second et le troisième état excité ainsi que leur dégénérescence.

        2^ème état excité : e₂₂₁ = e₂₁₂ = e₁₂₂ = 9 e_o      dégénérescence : 3
        3^ème état excité : e₃₁₁ = e₁₃₁ = e₁₁₃ = 11 e_o     dégénérescence : 3

Les entiers n_x, n_y et n_z doivent être strictement positifs. Aucun d'entre eux ne peut être nul, et ce à cause du principe d'incertitude de Heisenberg, pour les mêmes raisons que celles invoquées avec l'oscillateur harmonique. En effet, la particule étant localisée dans la boîte, Dx, Dy ou Dz sont au plus de l'ordre de L ; ainsi, Dp_x, Dp_y et Dp_z ne peuvent être nuls. L'énergie associée à chaque degré de liberté ne peut être nulle, ce qui implique que les nombres quantiques sont des entiers strictement positifs.

Il reste à analyser, sur un problème pratique, les conditions d'application de ces modèles microscopiques. Nous allons voir que, pour la plupart des systèmes macroscopiques, il n'est pas nécessaire d'avoir recours à la mécanique quantique et qu'un traitement classique peut constituer une approximation suffisante. Plaçons-nous dans le cadre d'un problème typique de physique statistique, celui des gaz parfaits, et considérons de l'hélium. C'est un bon exemple de gaz parfait, car chaque atome d'interagit que très faiblement avec ses voisins. Son énergie interne est donc d'origine purement cinétique. Prenons-en une mole (soit environ 4 g et 6,02.10²³ atomes) à la température T = 273 K et à pression atmosphérique P = 10⁵ Pa dans un récipient cubique de côté L. L'équation d'état des gaz parfaits nous conduit à

D'un point de vue macroscopique,  le récipient cubique contient un ensemble de particules libres indépendantes de très petite taille auxquelles la mécanique quantique attribue des énergies réparties suivant des valeurs discrètes qui sont égales à des multiples entiers de fois e_o définie par

où m représente la masse d'un atome d'hélium. Pour déterminer l'ordre de grandeur des nombres quantiques (n_x,n_y,n_z) des niveaux que vont peupler les atomes de gaz, nous allons utiliser les propriétés macroscopiques de celui-ci : le premier principe de la thermodynamique et l'expérience de Joule nous ont montré que l'énergie interne d'un gaz parfait ne dépend que de sa température. En fait, nous verrons par la suite que l'énergie cinétique moyenne d'un atome d'hélium à la température T est égale à

où k = R/N_A représente la constante de Boltzmann. Cette énergie est de l'ordre de 5,65.10^-21 J (soit 3,5.10^-2 eV) et est donc considérablement plus élevée que e_o. Si l'on suppose que n_x = n_y = n_z, on trouve 3 n_x² e_o = <e> soit n_x ~ 4.10⁹ ! Les nombres n_x, n_y et n_z sont donc considérablement grands. On peut montrer dans ce cas que la mécanique classique constitue une excellente approximation de la mécanique quantique. Par conséquent, l'évolution d'un atome d'hélium dans les conditions normales peut être décrite à l'aide de concepts classiques.

Remarque : la valeur de eo