Le quantum d'action

A relire aujourd'hui le Traité de chimie de Lavoisier - rédigé il y a deux siècles -, on y remarque aussitôt le rôle essentiel que son auteur attribue dans la constitution des corps à ce qu'il appelle le calorifique. Constatant que tous les corps de la nature sont "solides ou liquides ou dans l'état élastique et aériforme (gazeux)" suivant le degré de chaleur auxquels ils sont exposés, Lavoisier suggère qu'il est difficile de concevoir ces phénomènes "sans admettre qu'ils sont l'effet d'une substance réelle et matérielle, d'un fluide très subtil qui s'insinue à travers les molécules de tous les corps" et les écarte. Nous donnant une leçon de prudente sagesse, il ajoute toutefois que "nous ne sommes pas obligés de supposer que le calorifique soit une matière réelle ; [on peut] en envisager les effets d'une manière abstraite et mathématique.
Nous avons fait du quantum d'action l'acteur principal des interactions dans l'atome et nous lui avons donné l'habit d'une Idée de Démocrite, retrouvant en somme certains aspects de la pensée de Lavoisier. Mais s'agit-il là d'une simple manière de voir - différente en apparence seulement du point de vue habituel de la mécanique quantique ? - ou bien d'une nouveauté peut-être fondamentale entraînant des conséquences vérifiables ? Essayons, pour commencer, de comprendre ce qui, en termes "modernes", rend "insécable" notre quantum d'action.

Insécable, pourquoi ?

Désireux d'améliorer son hypothèse, Max Planck publie en 1906 ses Leçons sur le rayonnement thermique. Il y définit ce qu'il appelle "un domaine élémentaire de probabilité" et explique qu'en raison du théorème de Liouville, tout domaine de probabilité, considéré un instant quelconque, "est invariant par rapport au temps". Puis il écrit : "L'hypothèse des quanta d'action consiste à supposer que ces domaines, tous égaux entre eux, ne sont plus infiniment petits, mais finis et (égaux) à h, h étant une constante."
Ne pouvant tout aborder, je n'expliquerai pas ici en détail ce qu'il faut entendre par "domaine élémentaire de probabilité" et par "théorème de Liouville", mais je montrerai l'usage qui a pu être fait de ces concepts.
Dans son article sur "L'hypothèse des quanta" dont nous avons déjà parlé, Poincaré, reprenant la question, écrit : "Il faut que je cherche à éclaircir ce que sont les domaines de probabilité". Intervient alors la phrase clé : "ces domaines sont indivisibles" et il explique pourquoi : "Dès que nous savons que nous sommes dans un de ces domaines, tout est par là déterminé ; sans quoi, si les événements qui doivent suivre [...] devaient différer selon que nous nous trouverions dans telle ou telle partie de ce domaine, c'est que ce domaine ne serait pas indivisible [...] puisque la probabilité de certains événements futurs ne serait pas la même dans ses diverses parties".

Voici un usage que l'on peut faire de cette brillante analyse de Planck et de Poincaré : le quantum d'action progresse dans le vide en franchissant des "pas", chaque "pas" étant "un domaine élémentaire de probabilité", à la manière de Liouville-Planck, ce qui le rend indivisible, à la manière de Poincaré. Nous avons ainsi transféré au mouvement l'insécabilité attribuée par Démocrite à ses Idées !

Cette façon de voir entraîne des conséquences intéressantes. Soit L la longueur du pas, d le temps mis pour franchir un pas, p et E la quantité de mouvement et l'énergie transportées par le quantum. Le pas étant insécable, on aura alors pour chaque pas :
                                                                            L x p = 1    et    E x d = 1
Si la vitesse de propagation est v, alors en outre L = v x d.
Notons que, d'après ces formules, longueur du pas et quantité de mouvement transportée ont partie liée : plus le pas est long, plus la quantité de mouvement transportée est petite. De même, durée de temps pour franchir un pas et énergie transportée ont partie liée : plus la durée du pas est courte, plus l'énergie transportée est grande. Ces résultats correspondent à ce que l'on appelle en mécanique quantique le "principe d'incertitude".

Serait-il possible d'affirmer que les pas franchis par le quantum d'action dans le vide se font d'une manière que Démocrite et Descartes avec sa boule 1234 n'auraient pas désavouée ?

Le spin revisité

Revenons au problème du spectre. Le mécanisme par lequel l'atome fait un "saut quantique" est régi, nous l'avons vu, par une mystérieuse "règle de sélection" qui interdit à l'atome de faire n'importe quel saut. Or, cette règle, pour l'essentiel, a quelque chose de simple : seuls sont "permis" les sauts dans lesquels un électron de l'atome voit sont nombre quantique l changer d'une unité. Cette règle s'explique à merveille si l'on tient compte du fait que le quantum d'action tourne ou "tourbillonne" sur lui-même et possède un spin : lorsque l'atome émet (ou absorbe) un quantum d'action, le quantum emporte (ou apporte) avec lui, de par son spin, une unité d'action de rotation obligeant le l de l'atome, qui mesure une rotation, à changer d'unité. D'où la fameuse règle de sélection.
L'existence du spin entraîne un feu d'artifice de conséquences diverses. Etonnons-nous tout d'abord du fait lui-même : le quantum d'action est une particule qui "tourbillonne" éternellement sur elle-même dans le vide ! Notons ensuite que le spin, comme le pas, correspond à une unité d'action. Un tour de spin équivaut donc au franchissement d'un pas. Nous retrouvons là l'idée de la "boule qui roule" de Descartes. Il y a mieux encore : le spin peut prendre deux valeurs (notées +1 et -1) correspondant au fait que le quantum peut tourner sur lui-même "dans le sens des aiguilles d'une montre" ou dans le sens inverse. Un dernier détail : le spin introduit de façon naturelle la notion de phase dans la description du mouvement, notion indispensable pour la compréhension du phénomène des interférences comme nous le verrons plus loin.

L'électron, lui aussi, possède un spin, mais sa valeur, nous l'avons vu, est demi-entière. Que faut-il en conclure ? Qu'à l'encontre du quantum d'action, il faut à l'électron deux tours de spin pour compléter un pas. Mais pourquoi cette différence ? Mystère. Les physiciens se contentent de dire que l'électron (comme le neutrino et comme les quarks) est un fermion (particule à spin demi-entier) alors que le médiateur de la force électromagnétique (pour nous, le quantum d'action) est un boson (particule à spin entier). Aucune explication théorique de cette différence n'a encore été trouvée.

Les impulsions en orbe

Le 3 juin 1663, la Royal Society de Londres, nouvellement instituée, admet parmi ses membres un nouveau venu. Il s'appelle Robert Hooke (1635-1703), est âgé de 28 ans et a fait parler de lui depuis plusieurs années par la richesse de son ingéniosité. Deux ans plus tard, Hooke publie sa magnifique Micrographia, agrémentée de cinquante-sept dessins gravés sur cuivre par l'auteur, dans laquelle nous pouvons lire cette phrase prémonitoire : "Le mouvement de la lumière se propage en milieu homogène par des impulsions en orbe de force constante et qui agissent perpendiculairement à la direction de propagation."

Cette phrase nous apprend comment le quantum d'action - cette "impulsion en orbe" - agit sur les électrons qu'il rencontre : il leur fait subir une petite poussée perpendiculairement à sa direction de propagation. C'est l'effet principal (effet mystérieux s'il en est et pour lequel nous n'avons pas l'ombre d'une explication). Je me dois d'ajouter,pour être complet, que le quantum exerce également une "pression" dans la direction de son mouvement. Cette pression est habituellement interprétée comme l'effet "magnétique" (l'effet principal étant l'effet "électrique"). Voici un exemple spectaculaire de ce que l'effet principal entraîne. Un courant électrique traverse un fil conducteur. Le fil s'échauffe. Pourquoi ? Parce qu'il absorbe des quanta qui, venus de tous les points de l'espace, tombent perpendiculairement sur lui, transmettant à angle droit leur "poussée" aux électrons du courant qui parcourt le fil.

Il nous reste à aborder ce que j'appellerai "le mystère fondamental de la mécanique quantique". Dans son ouvrage La nature de la physique, publié en 1965, année où il reçut le prix Nobel, Richard Feynman le définit ainsi : "Je vais vous raconter l'expérience des deux fentes. Elle contient le mystère général, je n'évite rien, je dévoile la nature sous son aspect le plus élégant et le plus difficile."

Le mystère fondamental

Enoncé dans le langage de la mécanique du pas, ce mystère se résume à ceci : lorsque ceux particules de même nature arrivent ensemble sur une cible, elles sont efficaces (c'est-à-dire produisent un effet) si elles arrivent "hors phase". On dit dans ce cas qu'il y a eu "interférence" (mot dérivé de l'anglais to interfere, utilisé pour décrire le pas d'un cheval qui cogne ou "interfère" ses sabots l'un contre l'autre).

Signalons toutefois une difficulté, "la" difficulté : le phénomène se produit même si les particules arrivent isolément (une par une) sur la cible. Comment expliquer dans ce cas que des interférences puissent se produire ? Réponse : au Laboratoire fédéral des Etats-Unis, à Los Alamos, en 1982, Wojciech Zurech analyse ce qu'il appelle "l'effet de décohérence" selon lequel, lorsque des particules "suffisamment grosses" arrivent sur un cible, les particules de l'environnement - "le rayonnement ambiant, lumineux ou thermique" - empêchent les interférences de se produire.
J'emploierai cet argument... à l'envers. Lorsque les particules qui arrivent sur la cible sont suffisamment petites - des quanta d'action ou des électrons par exemple -, les particules de l'environnement permettent aux interférences de se produire.
Les interférences produisent le principe de moindre action dont nous avons parlé. Prenons l'exemple de deux électrons échangeant des quanta au sein d'un atome. Si l'on songe qu'un électron-volt correspond à quelques 2 400 milliards de quanta d'action par seconde, avec une énergie interne équivalente à 511 000 eV, chaque électron constitue une réserve quasi inépuisable de quanta à échanger. Mais les quanta interfèrent pour la plupart les uns avec les autres, et donc ne contribuent en rien à l'interaction. Seuls y contribuent effectivement ceux qui suivent des trajectoires leur permettant d'arriver "en phase" ensemble. Il se trouve que ces trajectoires sont celles pour lesquelles l'action est "la moindre".On obtient en fin de compte ce que Feynman appelle l'amplitude du processus considéré, somme totale des contributions de l'ensemble des quanta. Si l'amplitude est nulle, l'interférence est totale et le processus ne produit aucun effet détectable.
 

Pour Platon, nous l'avons vu, les "particules élémentaires" sont des triangles, ce qui permet de les assembler pour construire des atomes ayant la forme de polyèdres. Pour la mécanique quantique, aujourd'hui, les particules sont des points ; mais quelques-uns des meilleurs physiciens en cette fin de siècle s'efforcent de mettre au point une théorie qui en ferait des objets unidimensionnels, minuscules, caractérisés par une longueur L et une tension T - objets qu'ils ont baptisés "cordes" (supercordes dans une version de la théorie). Que deviendrait notre quantum d'action si cette théorie devait prévaloir ?

Lorsqu'une corde se déplace dans le vide, le parcours qu'elle décrit ressemble à un ruban (à un "tube" si la corde forme une boucle). Pour obtenir l'action, on est donc amené à multiplier la surface du ruban déroulé (qui mesure la "longueur" du trajet dans cette théorie) par la tension de la corde avant de diviser le tout par h - procédure qui revient à diviser la surface du ruban en "pas élémentaires" correspondant à de véritables "empreintes de semelle", ces empreintes devenant les unités d'action de la théorie des cordes. En un mot, si tout cela devait se réaliser, nous aurions un quantum d'action rénové ayant l'allure d'une petite surface, insécable bien entendu, de magnitude L².

Une telle théorie, si elle devait aboutir, nous rapprocherait du point de vue premier des Abdéritains, pour lesquels les Idées insécables étaient tout sauf des points ! Qui plus est, outre l'objet lui-même - la corde -, la donnée fondamentale en théorie des cordes est... l'action. Trouver une formule pour l'action correspondant au mouvement d'une corde dans l'espace-temps en est l'un des problèmes principaux.

Perspectives

Selon la mécanique quantique, les rayons émis (ou absorbés) par un atome sont composés de photons dotés, en tant que tels, de deux caractéristiques fondamentales : ils se déplacent à la vitesse de la lumière et ils transportent chacun un paquet d'énergie hn proportionnel à la fréquence n du rayon considéré.
Les choses se présentent différemment dans notre représentation. Les rayons sont composés de quanta d'action auxquels ni l'une ni l'autre des deux contraintes citées ci-dessus n'est applicable : les quanta peuvent aller soit moins vite soit plus vite que la lumière et peuvent transporter une énergie soit plus petite soit plus grande que hn. Y a-t-il une chance concrète de pouvoir trancher entre les deux points de vue, en observant par exemple un quantum allant plus vite que la lumière, et transportant une énergie plus grande que hn ?

Selon notre point de vue, lorsqu'un quantum rencontre sur son chemin un passage étroit - un tunnel - dont la largeur ou le diamètre est du même ordre de grandeur que la longueur de son pas, il "allonge son pas" pour traverser cet obstacle, ce qui a pour effet de le faire émerger de l'autre côté du piège plus tôt que prévu : il traverse donc le tunnel à une vitesse "supraluminique". Ce phénomène remarquable est connu en mécanique quantique sous le nom "d'effet tunnel". Au cours des années 1990, plusieurs groupes de chercheurs - en particulier Anedio Ranfani à Florence, Günter Nimtz à Cologne ou Raymon Chiao à Berkeley - l'ont étudié au moyen de techniques très sophistiquées. Ainsi, l'équipe de Cologne a mesuré des vitesses cinq fois supérieures à c !

Le phénomène fascine... et embarrasse les physiciens : c'est qu'ils sont habitués à penser que "rien ne peut aller plus vite que la lumière". Pour expliquer les vitesses supraluminiques, la mécanique quantique a recours à une représentation du photon qui en fait un "paquet d'ondes", véritable composite... d'éléments individuels ressemblant étrangement à nos quanta d'action ! En un mot, elle utilise de facto la représentation décrite ci-dessus.

Un paquet d'ondes embarrassant

A Berkeley, Aephraïm Steinberg a étudié de plus près le comportement d'un paquet d'ondes traversant un tunnel constitué dans ses expériences par une couche mince réfléchissante que seul un quantum sur cent en moyenne parvenait à traverser. Ses conclusions confirment qu'en traversant le tunnel le paquet "voyage plus vite que la lumière", même s'il conclut également "qu'on ne peut pas exploiter cet effet pour transférer de l'énergie à une vitesse moyenne supérieure à celle de la lumière". A quoi cela tient-il ?
Les calculs de Richard Feynman montrent que sur de longues distances, seuls les quanta qui se déplacent à la vitesse de la lumière parviennent à demeurer en phase les uns avec les autres et sont donc observables (sont "réels" pour les spécialistes). C'est ce qui nous fait dire que la lumière a une vitesse c bien déterminée, toujours la même dans le vide. Mais cette restriction ne s'applique pas sur de courtes distances, à l'échelle interne de l'atome par exemple.

Parviendrons-nous un jour à obtenir d'un atome qu'il nous fournisse des quanta allant plus vite que la lumière et restant en phase les uns avec les autres sur de longues distances ? Ou bien sommes-nous confrontés là à une impossibilité fondamentale, partie intégrante du système de la nature, comme le suggère la mécanique quantique ?

La parole est aux experts de l'optique quantique. L'avenir dira ce qu'il en est.

Pour finir

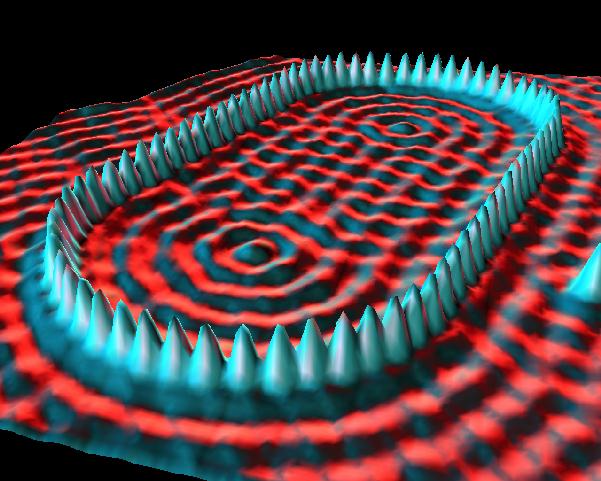
Par le biais de techniques ultramodernes mises au point au cours des dernières décennies, les physiciens ont réalisé d'étonnants travaux de type artisanal utilisant l'atome. Ainsi, par "l'écriture atomique", les chercheurs du centre IBM à Almaden ont dessiné avec trente-cinq atomes de xénon le sigle de leur compagnie sur une surface de nickel ; ont créé un "corral quantique" composé de quarante-huit atomes de fer positionnés sur une surface de cuivre ; ont construit un "volcan" de sept atomes de xénon déposés sur une surface de platine... et ont accompli bien d'autres merveilles.

Oui, l'atome, avec ses mystères, est bien comme nous l'avons dit dès le début, l'une des Sept Merveilles du monde : mystérieux, suspendu, creux, insolite, dominateur, froid, voyant... Voyant ? "Dessine-moi un atome", aurait pu demander le Petit Prince. Mais qui a jamais vu un atome ?

Les physiciens de l'Ecole Normale Supérieure à Paris, parmi d'autres, ont vu un atome ! Quoi de plus approprié, pour finir, que d'imaginer à notre tour l'atome que ces physiciens ont vu, point minuscule, perdu au milieu de la page...

Le principe du microscope à effet tunnel

Une exploration du principe de moindre action