Les ondes mécaniques
La dualité onde-corpuscule de la lumière

1 – Les ondes mécaniques progressives

            a – Quelques exemples

Propagation d’une perturbation dans un milieu à une dimension : la corde
Si on attache l’extrémité d’une corde à un support fixe (mur) et si l’on impose une perturbation de l’autre côté de la corde, la perturbation se propage le long de la corde, d’une extrémité à l’autre sans transport de matière.
On dit qu’une onde mécanique a été transmise le long de la corde.
Le milieu de propagation est la corde ; il est unidimensionnel. Ce milieu est par ailleurs élastique parce qu’il retrouve son été initial après avoir été temporairement déformé.
La direction de propagation de l’onde est celle de la corde.
Avant de retrouver sa position d’origine, un point de la corde se déplace perpendiculairement à la corde : on dit que l’onde est transversale.

En regardant "en coupe", on voit que le bateau bouge verticalement au passage de la vague : cette dernière se comporte comme une onde transversale ici.

Une onde est transversale lorsque le déplacement des points du milieu de propagation s’effectue perpendiculairement à sa direction de propagation.

Propagation d’une perturbation dans un milieu à une dimension : le ressort
On accroche un ressort à une extrémité fixe, on comprime quelques spirales et on lâche : la propagation se propage le long  du ressort, d’une extrémité à l’autre, sans transport de matière.
Une onde mécanique a été transmise le long du ressort.
Le milieu de propagation est unidimensionnel, la direction de propagation est l’axe du ressort.
Une spire du ressort se déplace parallèlement à l’axe du ressort avant de revenir à sa position d’équilibre. On dit que l’onde est longitudinale.

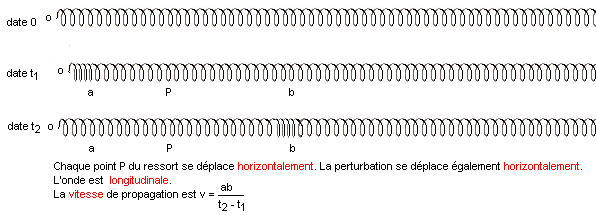
Une onde est longitudinale lorsque le déplacement des points du milieu de propagation s’effectue parallèlement à sa direction de propagation.

Propagation d’une perturbation dans un milieu à deux dimensions : la pierre et l’étang
Lorsqu’on jette une pierre dans l’eau d’un étang, une perturbation se propage, à partir du point de chute, sous forme d’une ride circulaire.
Le milieu de propagation est le plan de l’eau : c’est un milieu à deux dimensions. Une perturbation se propage dans toute direction issue du point-source S et contenue dans le plan de l’eau.

NB : en cours, on utilise la cuve à ondes pour recréer le phénomène.

Propagation d’un son dans un milieu à trois dimensions
Quand on produit un bruit (perturbation sonore de courte durée) celui-ci se propage, à partir du point-source S, dans toutes les directions de l’espace. Une perturbation de nature sonore se propage dans un milieu tridimensionnel.
Le principe de propagation est le même que pour le ressort : ce sont les couches d’air qui jouent le rôle des spires ; elles sont alternativement comprimées et détendues.

            b – Définitions

Dans tous les exemples précédents, un point du milieu matériel atteint par la perturbation subit un déplacement et revient à sa position initiale. La propagation se déplace donc sans transport de matière.

On appelle onde mécanique le phénomène de propagation d’une perturbation dans un milieu matériel sans transport de matière .

On utilise l’expression onde progressive pour bien marquer le fait que la perturbation progresse dans un milieu élastique.
La propagation d’une telle onde dans un milieu s’effectue avec une certaine « vitesse », mais puisqu’elle s’effectue sans transport de matière, on préfère utiliser le terme « célérité ».
La célérité v d’une onde est le rapport entre la distance parcourue par l’onde et la durée Dt du parcours

où v est la célérité de l’onde, en m.s^-1
     d est la distance parcourue par l’onde, en m
     Dt est la durée du parcours, en s

Par exemple, la célérité d’une onde le long d’une corde élastique ou à la surface de l’eau est de l’ordre de quelques dizaines de m.s^-1.
Pour la mesurer, on peut utiliser deux capteurs repérant le passage de l’onde, séparés d’une distance d, et un chronomètre mesurant la durée Dt entre les deux passages.

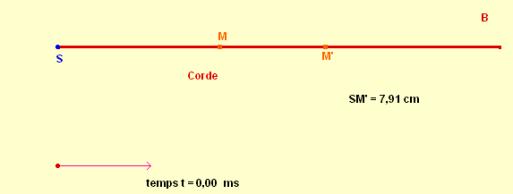
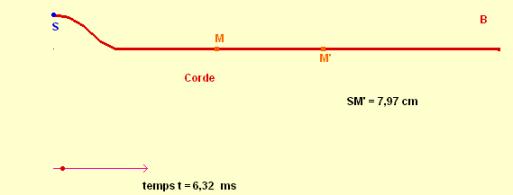
Considérons la propagation d’une onde le long d’une corde (milieu unidimensionnel) ; on produit une perturbation au point S qui se propage le long de la corde, parvient au point M’ puis au point M.  

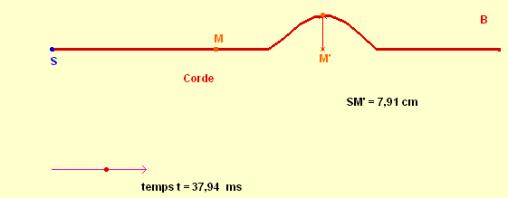Si la propagation se fait sans amortissement, la perturbation en M’ reproduit la perturbation en S mais avec un certain retard,

si v est la célérité de l’onde.
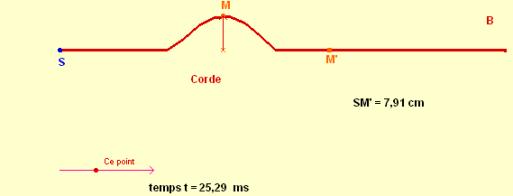
De la même façon, la perturbation au point M à la date t est la perturbation qui existait au point M’ à la date antérieure t’ = 1 - t’ où

En conclusion : dans une onde mécanique, tout point du milieu subit la même perturbation que la source, avec un retard.

         c - Propriétés

Une onde se propage dans toutes les directions qui lui sont offertes
Dans un milieu unidimensionnel, il n’existe qu’une seule direction de propagation.
Dans un milieu bidimensionnel, tel un plan, l’onde se déplace dans toutes les directions contenues dans ce plan à partir de la source.
Dans un milieu tridimensionnel, l’onde progresse dans toutes les directions de l’espace issues du point-source.

Une onde réalise une transfert d’énergie mécanique sans transport de matière
Pour produire la perturbation, il faut fournir de l’énergie mécanique ; la perturbation se propage, 
chaque point de la corde revenant à sa position initiale après le passage de l’onde. 
Il n’y a donc pas de transport de matière. 


Remarque : l’énergie mécanique ne se conserve pas forcément pour autant, car à cause 
de frottements divers, l’énergie transportée diminue ; cela se traduit par une diminution 
de l’amplitude au cours de la progression de l’onde.

La célérité d’une onde est une propriété du milieu de propagation
Dans un milieu élastique déterminé, la célérité d’une onde est constante. Par exemple, la célérité du son dans l’air à 15°C sous 1,0 bar est voisine de 340 m.s^-1.
La célérité d’une onde dépend des propriétés du milieu : par exemple, la célérité du son dans l’air dépend de la température.

2 – Ondes progressives périodiques

            a – Un phénomène doublement périodique

On utilise un vibreur, c’est-à-dire une lame de métal qui vibre par l’intermédiaire d’un électroaimant alimenté par un générateur de courant alternatif, généralement sinusoïdal.
Lorsque l’électroaimant fonctionne, l’extrémité S de la lame vibre et effectue des oscillations périodiques autour de sa position d’équilibre.

La période T des oscillations est la durée d’une oscillation ; elle s’exprime en secondes.
La fréquence f est l’inverse de la période :

Il s’agit en fait du nombre d’oscillations effectuées en 1 s ; elle s’exprime en hertz (Hz) et multiples (kHz, MHz, GHz).

Si l’on relie le vibreur à l’extrémité libre d’une corde arrimée à un point fixe, on observe un mouvement particulier, que l’on peut étudier par chronophotographie ou stroboscopie. L’aspect de la corde est une sinusoïde, et chacun de ses points effectue des oscillations dans la direction verticale avec une amplitude constante.
Avec le stroboscope, lorsque la corde paraît immobile, tous ses points effectuent entre deux éclairs consécutifs une ou plusieurs oscillations complètes et apparaissent toujours dans la même position : tous les points de la corde vibrent avec la même fréquence que la source S.

Une première périodicité apparaît, caractérisée par la période T : on parle de périodicité temporelle.

  En utilisant l’éclairage stroboscopique permettant d’observer le mouvement « au ralenti », on observe que certains points ont le même mouvement que d’autres : ils passent à leur position d’équilibre ou à leurs écartements maximum aux mêmes instants. On dit qu’ils vibrent en phase. Par ailleurs, ils sont régulièrement répartis sur la corde : on note l et on appelle longueur d’onde la distance séparant deux points consécutifs vibrant en phase.

La corde immobilisée par effet spectroscopique a l’allure d’une sinusoïde de période l : il apparaît une deuxième périodicité, une périodicité spatiale de longueur caractéristique l.

Relation entre longueur d’onde l et période T

A la date t₁, disons que l’onde atteint le point F (qu’on appelle front de l’onde) ; ce point F commence alors à vibrer et l’onde se propage.

A la date t₁+T, une période plus tard, les points F et F’ vibrent en phase, leur distance est donc une longueur d’onde l

FF’ = l

Par ailleurs, puisque l’onde se propage à la célérité v,

FF’ = v.T

On en déduit

l = vT

B - Onde progressive périodique à la surface de l’eau
On utilise la cuve à ondes pour illustrer le phénomène.

En éclairage normal, on voit des rides circulaires sombres et claires (suivant l’épaisseur d’eau que traverse la lumière) qui se propagent à partir de la pointe.

En éclairage stroboscopique, à fréquence convenable, on voit des rides circulaires uniformes (cf. ci-dessus). Le cliché met en évidence la périodicité spatiale, puisque tous les points situés sur une ride vibrent en phase ; deux rides claires (ou deux sombres) sont séparés par la distance l.

            c – Dispersion et propagation des ondes

Dans une onde progressive comme l’onde plane à la surface de l’eau, tous les points du milieu vibrent parce que le mouvement de la source S leur est transmis de proche en proche. La propagation de ce mouvement s’effectue à vitesse constante v dans des conditions déterminées : par exemple, si l’on augmente l’épaisseur d’eau de la cuve, la célérité varie.

Si l’on mesure la célérité pour différentes valeurs de la fréquence de vibration de la source, on constate que cette célérité dépend de cette fréquence : on dira que le milieu est dispersif.

L'excitateur utilisé ici est une plaque plane : l'onde obtenue est plane. Nous voyons que si la fréquence de l'onde varie, sa célérité varie également : le milieu est dispersif.

Un milieu sera dit non dispersif si la célérité des ondes dans ce milieu ne dépend pas de la fréquence de l’excitation.

Plaçons sur le trajet de ces ondes planes de longueur d'onde l fixée une fente réglable. Suivant la largeur de cette fente, on observe des figures étonnantes.

On réalise une fente en plaçant deux plaques de plexiglas que l'on rapproche plus ou moins : à gauche, la fente est moins étroite qu'à droite.

L’onde plane est déformée au passage de la fente : elle continue à se propager, mais devient plus ou moins circulaire, d’autant plus que la fente est étroite.

On dit que l’onde est diffractée par la fente.

Nous avons vu que le son était une onde mécanique ; comme les ondes à la surface de l’eau, elle se diffractent : ainsi, une personne située dans une pièce entend qu’on l’appelle depuis une autre pièce même si elle n’est pas en face de l’ouverture entre les deux pièces. Ceci s’explique car les ondes sonores graves ont une longueur d’onde de quelques mètres et sont ainsi diffractées par la porte dont l’ouverture est de l’ordre de grandeur voire plus petite que cette longueur d’onde. En revanche, les ondes sonores aiguës ont une longueur d’onde de quelques centimètres et sont seulement « diaphragmées » par la porte : on dit qu’elles sont directives.

En résumé : on observe la diffraction d’une onde lorsqu’elle traverse une ouverture dont la largeur est du même ordre de grandeur, voire inférieure, à sa longueur d’onde l.

3 – Le modèle ondulatoire de la lumière

            a – Diffraction de la lumière
Réalisons l’expérience suivante.

Si le diamètre de la fente est de l’ordre du dixième de millimètre, on observe la figure suivante.

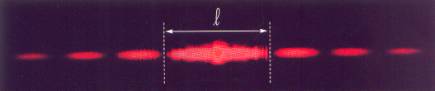
On obtiendrait un résultat similaire si l’on avait utilisé un cheveu ou un fil.
Le résultat est un peu différent si l’on utilise un trou plutôt qu’une fente ou un fil.

De même, si l’on utilise une ouverture carrée :

            b – Propagation de la lumière dans le vide

Les ondes mécaniques présentent la propriété d’être diffractées lorsqu’elles rencontrent une ouverture de l’ordre de grandeur ou inférieure à la leur longueur d’onde.

La lumière présente la même propriété : il est donc logique de penser qu’elle se comporte, dans certaines conditions, comme une onde.
Dans le vide – comme, pratiquement, dans l’air – toutes les ondes lumineuses se propagent avec une célérité constante

C = 299 792 458 m.s^-1 » 3,0.10⁸ m.s^-1

Cette grandeur est une constante fondamentale et universelle de la Physique : elle permet de définir le mètre et fournit une limite infranchissable pour le déplacement de tout corps matériel.

  Une onde, ou radiation, lumineuse est caractérisée par sa longueur d’onde dans le vide

où T représente la période (en secondes) et n la fréquence (en hertz) de l'onde lumineuse. Il existe des ondes lumineuses de toutes fréquences ; on les rassemble dans ce qu'on appelle le spectre électromagnétique.

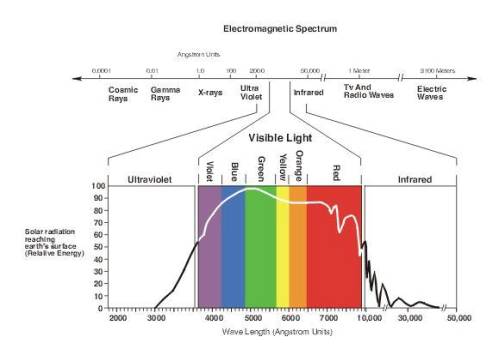
L’œil n’est cependant sensible qu’à quelques radiations lumineuses : le domaine de longueur d‘onde dans le vide des radiations visibles s’étend approximativement de 400 nm (violettes) à 800 nm (rouges) ; de part et d’autre s’étendent les radiations ultraviolettes (l(UV) < 400 nm) et infrarouges (l(IR) > 800 nm).
Les ondes radio sont des ondes lumineuses de très grande longueur d’onde (petite fréquence).
Les radiations X (celles de nos radios médicales) et gamma (notées g) sont des ondes lumineuses de très courte longueur d’onde (grande fréquence).

A une lumière de longueur d’onde bien déterminée dans le vide correspond une radiation élémentaire de couleur bien déterminée : on la qualifie de lumière monochromatique. Par exemple, le laser rouge He-Ne couramment utilisé au lycée émet une lumière monochromatique de longueur d’onde dans le vide l = 632,8 nm.

Une lumière polychromatique est constituée de plusieurs radiations monochromatiques : c’est le cas de la lumière blanche, constituée d’une infinité de radiations monochromatiques.

Retour sur la diffraction de la lumière
La figure de diffraction de la lumière laser par une fente (ou un fil) est essentiellement formée d’une tache centrale brillante de largeur d, observée sur un écran à la distance D de la fente.

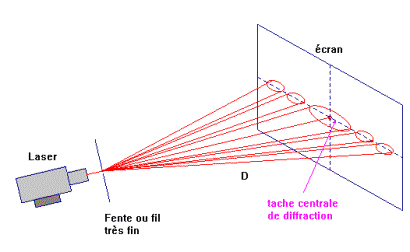
On appellera i l'écart angulaire entre le milieu de la tache centrale O et la première extinction M.

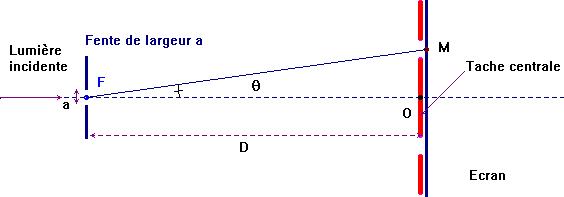
Nous pouvons voir que

où q s'exprime en radians (rad).
Par ailleurs, une étude théorique poussée conduit à la relation

Cette relation montre que plus la fente est étroite, et plus la tache centrale est large.

            c – Propagation de la lumière dans les milieux matériels transparents

La lumière se propage dans les milieux transparents tels que l’eau, le verre, le Plexiglas …

Si v est la célérité d’une onde lumineuse monochromatique dans le milieu considéré, on appellera indice de réfraction ou plus simplement indice de ce milieu pour la radiation considérée le nombre sans dimension

puisqu'aucun corps matériel ne peut aller plus vite que la lumière dans le vide.

En 1666, Newton fut le premier à réaliser une expérience de dispersion de la lumière blanche en faisant traverser un prisme en verre par cette lumière polychromatique.

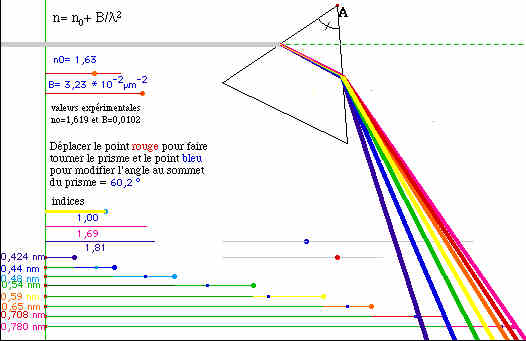
La lumière monochromatique du laser est déviée par le prisme.  
La lumière blanche est déviée et, en plus, le faisceau est étalé et présente les différentes couleurs de l’arc-en-ciel.

La lumière blanche est un « mélange » de toutes les lumière monochromatiques visibles. Le prisme décompose cette lumière et fait apparaître toutes les lumière monochromatiques qu’elle contient.

L’expérience de dispersion de la lumière montre que le trajet de la lumière dépend de sa couleur, c’est-à-dire de sa fréquence. La réfraction observée, et par conséquent l’indice de réfraction du verre, dépend de la couleur de la lumière : la lumière bleue est plus réfractée que la lumière rouge.

En conclusion : l’indice d’un milieu comme le verre dépend de la fréquence de la lumière qui s’y propage. On dit que le verre est un milieu dispersif, et on note la relation

n = n(n) = n(l)

Il faut donc préciser la valeur de l’indice pour les lumières de chaque couleur.
Exemple : pour le verre ordinaire,

n_rouge = 1,510

n_orangé = 1,515

n_violet = 1,520

4 - Caractère corpusculaire de la lumière

        a - Les observations
Tout part d'expériences d'optique. Des gens ont pensé à essayer de faire passer du courant dans des ampoules remplies de gaz atomique (hydrogène, par exemple) pour voir ce qui se passerait : pour de fortes différences de potentiel, ils se rendirent compte qu'ils avaient formé une lampe, plutôt rouge dans le cas de l'hydrogène.

Depuis Descartes, les lois de la réfraction lumineuse sont connues. On connaît l'action d'un prisme sur une lumière blanche, issue d'une ampoule classique à filament de tungstène chauffé : il décompose cette lumière en une succession de couleurs, qu'on retrouve dans l'arc-en-ciel. Cette figure constitue ce qu'on appelle le spectre de la lumière blanche ; il est continu, c'est-à-dire que toutes les couleurs s'entremêlent sans jamais se détacher.

Ce phénomène tient à la dispersion qu'offre le prisme, dont l'indice de réfraction n dépend de la fréquence de la radiation lumineuse qui ui est communiquée ; la deuxième loi de Descartes sur la réfraction, dépendant de ce nombre n, montre que les différentes fréquences sont donc réfractées avec des angles différents, d'où la figure observée.

En plaçant une fente puis un prisme devant une lampe à hydrogène, les scientifiques se sont rendus compte que le spectre obtenu était différent de celui de la lumière blanche : ils ont obtenu un spectre de raies.

        b - Les interprétations

Un long cheminement
L'interprétation de ce spectre mit des années à apparaître. Elle est venue avec la naissance de la mécanique quantique. Deux pas de géant ont été faits avec les deux découvertes suivantes :

• la loi de corps noir : un corps noir est un objet qui est capable de réémettre tout l'énergie qu'il reçoit. Par un raisonnement qui ne tient plus aujourd'hui, en travaillant sur les ondes, Max Planck a établi que l'énergie était répartie en quanta d'énergie, sortes de petites particules, de masse nulle, et chacune d'énergie (en joules)

            où h est la constante dite de Planck et n la fréquence exprimée en hertz.

• l'effet photoélectrique : de la lumière UV peut arracher des électrons à une plaque de métal ; ces électrons peuvent être détectés sous forme d'un courant, et Einstein a retrouvé l'interprétation des quanta de Planck : la lumière serait constituée de particules d'énergie sans masse, les {\bf photons}, qui sont capables en choquant les électrons du métal de leur donner assez d'énergie pour les soustraire à ce métal. L'observation du courant a montré que l'énergie nécessaire était "quantifiée" : chaque photon porte une énergie

Les spectres de raies
Ces deux avancées conceptuelles ont conduit aux premières idées sur la quantification de l'énergie des atomes.
Prenons le cas le plus simple de l'atome d'hydrogène, formé classiquement d'un proton et d'un électron gravitant autour ; ce système stable est caractérisé par une certaine énergie, en particulier celle de l'interaction entre les charges opposées de ces particules (force électrostatique coulombienne). C'est la forme de cette énergie atomique qui explique les spectres de raies obtenus.

Raisonnons sur l'électron : en effet, celui-ci ne peut occuper que des trajectoires (autour du proton) d'énergie déterminée, quantifiée, ne pouvant prendre n'importe quelle valeur : les raies lumineuses observées correspondent ainsi aux désexcitations de l'électron de niveaux d'énergie initiaux E_i vers des niveaux d'énergie (plus basse) finaux E_f reliés par la relation

où n est la fréquence du photon émis lors de la désexcitation (c'est-à-dire la fréquence de la raie, du rayonnement observés). Cette relation porte le nom de relation d'Einstein.
Il existe en fait deux types de spectres de raies :

• les spectres de raies d'émission : ce sont ceux obtenus par exemple lors de l'étude de lampes atomiques (à hydrogène, par exemple). Ils se présentent comme des raies continues sur fond noir, chacune correspondant à une transition entre deux niveaux d'énergie, par émission d'un photon dont la fréquence (donc la couleur dans le vide) correspond à l'énergie entre niveaux par la relation d'Einstein.

• les spectres de raies d'absorption : ce sont ceux observés lorsqu'on étudie les étoiles ou les nébuleuses dans l'espace. Ils se présentent sous forme de raies sombres sur un fond continu comportant toutes les couleurs : il semble donc que certaines radiations aient été absorbées. C'est ce qui se passe en fait, si l'on imagine que le fond continu est dû à une source de lumière blanche, et que l'absorption est due à un corps situé entre la source et l'observateur du spectre. Ce corps absorbe certaines radiations, en fonction de ses niveaux d'énergies, et le spectre que l'on détecte alors permet de caractériser ce corps. Dans le cas des étoiles, la lumière est produite par l'intérieur de l'astre puis absorbée par l'atmosphère de celui-ci avant de nous parvenir. Dans le cas d'une nébuleuse, le plus souvent, c'est la lumière d'étoiles proches qui filtre à travers cette poche de gaz que l'on étudie.

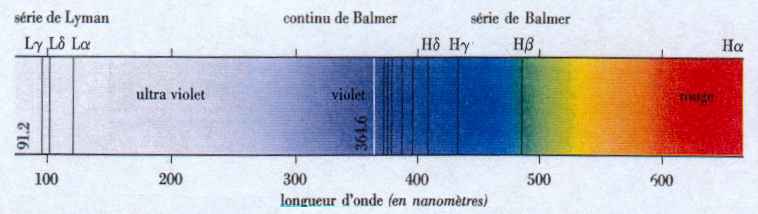Spectre d'absorption de l'atome d'hydrogène.

Il faut bien comprendre que le spectre d'un corps, en émission comme en absorption, est en quelque sorte sa signature. On est capable d'identifier les raies d'un spectre quelconque en les attribuant chacune à un élément chimique. C'est ainsi qu'on fonctionne par exemple en étudiant les spectres stellaires.

L'hydrogène, par exemple, présente une raie à la longueur d'onde de 21 cm.
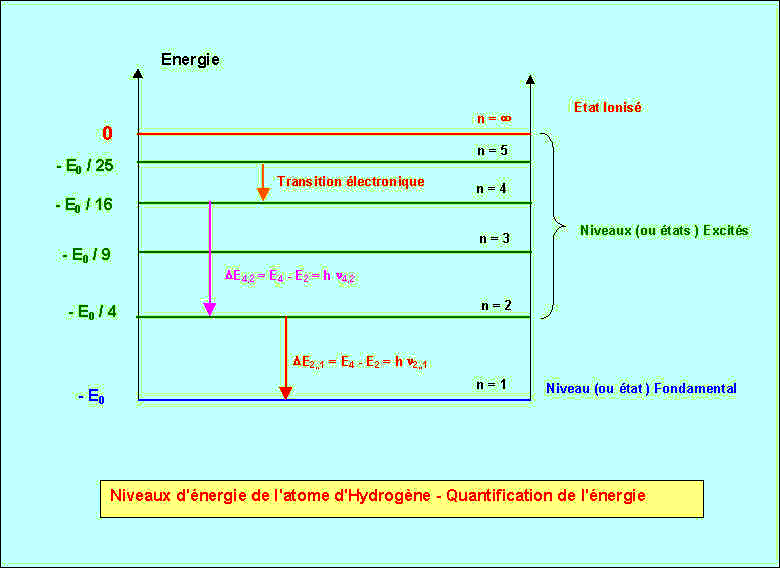
Voici successivement le spectre de l'hydrogène dans le domaine visible (série de raies de Balmer), puis ce qu'on appelle le diagramme énergétique de l'atome d'hydrogène, faisant apparaître les différentes transitions possibles (en émission) et les raies associées.

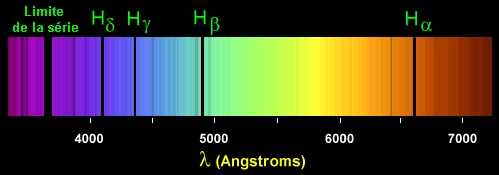Spectre de l'hydrogène dans le domaine visible. Les longueurs d'onde des raies observées correspondent à la série dite de Balmer (voir ci-dessous). En haut, le spectre d'absorption de l'hydrogène. En bas, son spectre d'émission. On note bien la différence entre les deux classes de spectres, raies sombres sur fond continu en absorption (les raies sont absorbées), raies colorées sur fond sombre en émission (les raies sont émises).

Original : de la spectroscopie avec une webcam !
Pour aller plus loin, avec le CLEA...

Retour aux questions de sciences