Résonance
Magnétique
Nucléaire



Une Introduction
 









DÉFINITION

Technique spectroscopique qui permet de détecter la présence de certains éléments chimiques par la mesure de l'absorption de l'énergie émise par une radiation électromagnétique du domaine des radio-fréquences, lorsque ces éléments sont placés dans un champ magnétique puissant.


1.1. PROPRIÉTÉS MAGNÉTIQUES DU NOYAU DE L'ATOME


Les particules comme les protons, neutrons et électrons ainsi que les noyaux de certains isotopes se comportent comme des corps tournant sur eux-mêmes, mouvement qui induit un moment angulaire de spin.

Les états de spin permis sont quantifiés et peuvent prendre 2I + 1 valeurs. D'une façon empirique, il est permit de trouver les valeurs de spin des noyaux des éléments.


Tableau 1

Propriétés magnétiques des noyaux des atomes
Masse atomique Numéro atomique I
impair pair ou impair 1/2, 3/2, 5/2...
pair pair 0
pair impair 1, 2, 3...



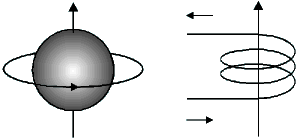
Figure 1.1. À gauche, dipôle magnétique induit par la rotation d'un proton. À droite, dipôle induit dans une bobine par le passage d'un courant.



En l'absence de champ magnétique les protons sont orientés au hasard . Placés dans un champ magnétique, le proton puisqu'il possède un moment angulaire de spin = 1/2 n'adopte que deux orientations correspondant à des niveaux d'énergie différents (figure 1.2). Une dont le moment magnétique est orienté parallèlement et l'autre antiparallèlement au champ magnétique appliqué H0 (diagramme figure 1.3).



Figure 1.2. À gauche, orientation des protons en l'absence de champ. À droite, en présence d'un champ magnétique. En bleu, les protons orientés dans le sens du champ et en rouge, les protons orientés dans le sens contraire au champ.



Si le champ magnétique est nul, les deux niveaux d'énergie sont égaux, sinon la différence entre les deux est: .
Un équilibre s'établit où des noyaux absorbent de l'énergie et passent d'une orientation parallèle à celle qui est antiparallèle au champ ou perdent de l'énergie dans la transition inverse.



Figure 1.3. Diagramme des niveaux d'énergie correspondant aux orientations de spin des protons.


Le temps mis pour atteindre cet équilibre varie exponentiellement avec T1 appelé temps de relaxation thermique qui dépend pour une part de l'agitation moléculaire elle-même fonction de la température et de la viscosité du milieu et d'autre part de la force des interactions entre les noyaux et le reste de l'échantillon, autrement dit des valeurs de m du proton et des autres atomes de l'échantillon.

À l'équilibre, le nombre de protons dont le moment magnétique est orienté dans le sens du champ est en léger excès; 10 sur 2000000 pour le noyau 1H à 300oK dans un champ de 14092 Gauss.



1.2. RÉSONANCE


Pour mieux comprendre le phénomène de résonance, il faut comparer le proton à une toupie en rotation subissant l'influence du champ de gravitation de la terre. En présence d'un champ appliqué, le moment magnétique ne s'oriente pas exactement dans la direction du champ mais s'en écarte par certain angle appelé angle de précession. Le moment magnétique décrit ainsi un mouvement circulaire perpendiculaire à la direction du champ.



Figure 1.4. Mouvement de précession d'une toupie en rotation dans le champ de gravitation de la terre et mouvement de précession d'un proton en rotation dans un champ magnétique.



Plus le champ magnétique est puissant plus la fréquence de précession est grande. Pour un proton dans champ de 14092 Gauss, la fréquence de précession est d'environ 60 MHz et dans un champ de 23500 Gauss, elle est de 100 MHz. Cette relation entre la fréquence et l'intensité du champ magnétique s'exprime comme ceci:


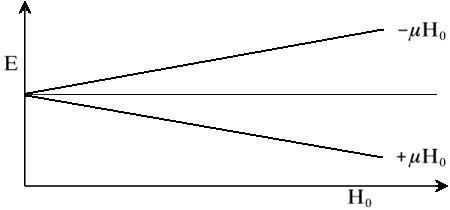
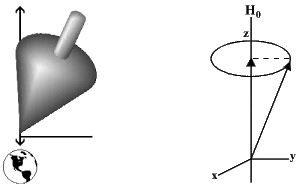
où H0 = intensité du champ magnétique
h = constante de Planck
n = fréquence de la radiation
g = rapport gyromagnétique caractéristique de chaque noyau




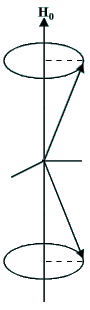
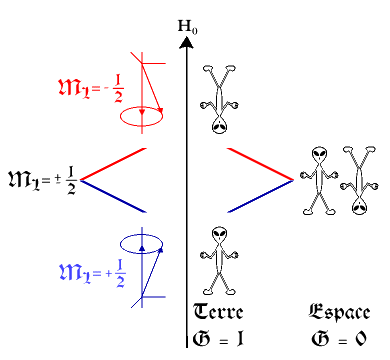
Figure 1.5. Le moment magnétique peut être orienté dans la direction du champ appliqué ou dans la direction opposée. Illustration qui tient compte du phénomène de la précession.


Comme le proton est chargé, le mouvement de précession génère un champ électrique oscillant à la fréquence de 60 MHz dans un champ magnétique de 14092 Gauss.


SI, DANS UN CHAMP DE 14092 GAUSS, UNE RADIATION DE FRÉQUENCE ÉGALE A 60 MHz EST ÉMISE, L'ÉNERGIE DE CETTE RADIATION EST ABSORBÉE PAR LE PROTON QUI PASSE A UN NIVEAU SUPÉRIEUR D'ÉNERGIE ET PAR LE FAIT MÊME CHANGE DE SPIN.

CE PROCESSUS EST APPELÉ RÉSONANCE, LE PROTON RÉSONANT AVEC LA RADIATION ÉLECTROMAGNÉTIQUE.



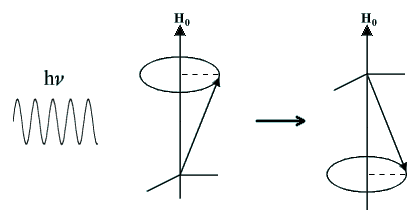
Figure 1.6. Proton dont le spin change d'orientation par l'absorption de l'énergie d'une radiation électromagnétique.



1.3. INSTRUMENTATION SIMPLIFIEE


1.3.1. SPECTROMÈTRE DE RÉSONANCE MAGNÉTIQUE NUCLÉAIRE

Pour qu'il y ait passage d'un état de spin à un autre d'un proton placé dans champ magnétique fixe, il faut faire varier la fréquence n; de la radiation électromagnétique de sorte que cette dernière soit égale à la fréquence de précession de ce proton.

Il est cependant plus facile de construire un appareil de fréquence fixe et de champ magnétique variable que l'inverse.


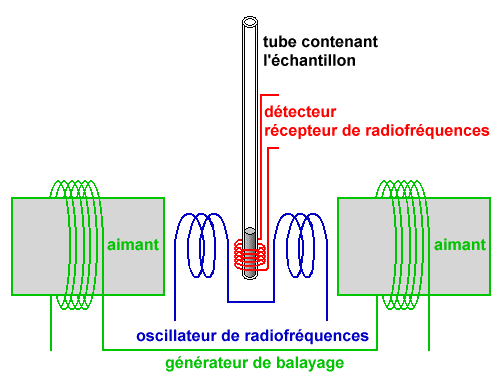
Figure 1.7. Schéma du spectromètre de RMN.


1.3.2. TUBES RMN

C'est une petite éprouvette de verre dont les dimensions (pour la RMN du proton) sont données ci-dessous. Elle est fabriquée avec précision puisqu'elle doit tourner.

longueur du tube: 18 cm.
diamètre externe: 5 mm
diamètre interne: 4 mm


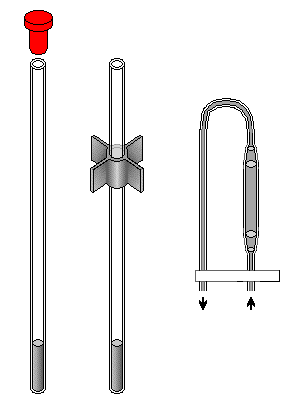
Figure 1.8. Tubes RMN. La turbine à air comprimé sert à faire tourner le tube. La hauteur du tube dans l'appareil est ajustée au moyen d'une jauge. Du coté droit il y un tube à travers lequel coule l'éluant avec le produit à analyser.


En effet la rotation du tube est nécessaire à l'obtention de spectres convenables. Si le tube ne tourne pas, les pics obtenus sont larges. Ceci est dû aux faibles variations de champ dans la solution.

Il faut donc trouver la vitesse idéale de rotation du tube (qui est approximativement 60 tours/sec pour un appareil de 60 MHz), afin que tout l'échantillon soit soumis au même champ magnétique.

Si le tube tourne trop vite, il y a apparition d'un vortex dans la solution (phénomène semblable au mouvement de l'eau qui s'écoule par un drain).


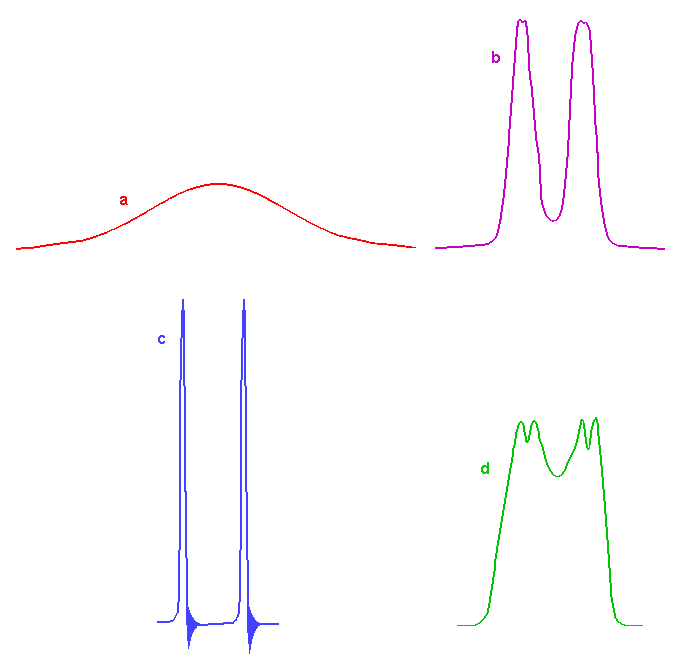
Figure 1.9. Allure des pics en fonction de la vitesse de rotation du tube: a) pas de rotation; b) vitesse trop lente; c) vitesse idéale; d) vitesse trop rapide.


1.3.3. LES SOLVANTS

La résonance magnétique nucléaire est moins sensible que l'infrarouge et beaucoup moins sensible que l'ultraviolet. Elle exige donc des solutions plus concentrées; de l'ordre de 20% pour le modèle courant.

Les solvants les plus utilisés sont ceux qui ne possèdent pas d'hydrogène comme le CCl4 et les solvants deutériés (dans lesquels les hydrogènes ont été remplacés par des deutériums).

Comme il est impossible d'obtenir des substances deutériées à 100%, il y a toujours sur le spectre les pics des protons résiduels des solvants deutériés.


Tableau 2

Solvant Formule Déplacement(s) chimique(s) des protons résiduels
tétrachlorométhane CCl4 --
disulfure de carbone CS2 --
benzène C6H6 7,37
chloroforme CDCl3 7,27
dichlorométhane CD2Cl2 4,80
acétone CD3COCD3 2,10
acétonitrile CD3CN 1,97
sulfoxyde de méthyle CD3SOCD3 2,52
eau D2O variable
pyridine C5D5N 8,50 7,35 6.98