2.1. DÉPLACEMENT (GLISSEMENT) CHIMIQUE




Le champ magnétique dans l'environnement immédiat du proton n'est pas strictement le même que le champ appliqué, sinon il n'y aurait qu'un pic pour un élément donné; ce qui enlèverait tout intérêt à cette technique.




2.1.1. BLINDAGE (SHIELDING)

Les électrons entourant un noyau produisent un champ magnétique secondaire qui s'oppose au champ appliqué. La constante de blindage (shielding constant) est définie comme étant directement proportionnelle à la densité du nuage électronique qui entoure le noyau. Si la densité d'électrons augmente, l'effet du champ magnétique sur le noyau décroît et, au contraire si la densité d'électrons diminue, l'effet du champ magnétique sur le noyau croît.



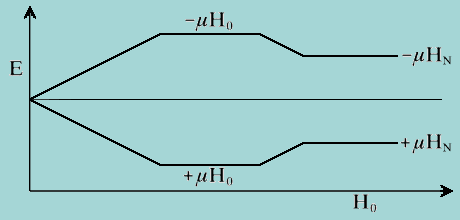
Figure 2.1. Comparaison des nivaux d'énergie d'un proton déblindé H0 et blindé HN dans un champ magnétique appliqué.



Le proton est soumis au champ appliqué suivant



La résonance se produit donc à





2.1.2. DÉPLACEMENT CHIMIQUE

Le déplacement chimique d'un proton est relié à la constante de blindage s et est définie comme



Les variations de champ magnétique sont exprimées en unités de fréquences car H0n où k = constante de proportionnalité et



Chaque proton dans une molécule est blindé à des degrés divers dépendant de son environnement électronique. Les différences entre les fréquences de résonance des différents protons d'une molécule sont très petites, entre 0 et 600 Hz dans un champ de 14092 Gauss, ce qui représente une fraction d'environ 0,001% de H0.

Arbitrairement, comme n et nréf sont des valeurs très grandes et très proches de n0 (la fréquence de la radiation électromagnétique), d devient une valeur sans dimension exprimée en ppm.



ex: si un proton absorbe à 120 Hz (sur un appareil de 60 MHz)



La fréquence de référence fixée à 0 d est celle des protons du tétraméthylesilane TMS, Si(CH3)4.

La notation t = 10,00 - d est aussi utilisée.

ex: si d = 2,00 ppm, t = 10,00 - 2,00 = 8,00 ppm.


2.1.3. DÉBLINDAGE DÛ L'ENVIRONNEMENT ÉLECTRONIQUE

Chaque proton dans une molécule est blindé à des degrés divers dépendant de son environnement électronique. Les différences entre les fréquences de résonance des différents protons d'une molécule sont très petites, entre 0 et 600 Hz dans un champ de 14092 Gauss, ce qui représente une fraction d'environ 0,001% de H0.


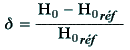
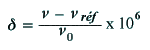
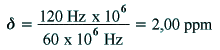
Figure 2.2. À gauche un proton dans un champ magnétique. À droite, le même système avec le champ produit par les électrons.


Le champ magnétique exercé sur le noyau est modifié par les électrons avoisinants de H0 à H0(1-s) où s = blindage.

Parce que le champ magnétique induit par les électrons Hé s’oppose au champ H0, l'effet est dit diamagnétique et est directement proportionnel à la densité électronique.

Pour le proton l'effet électronique (induction, résonance) décrit le rôle de la structure sur la densité électronique.


Un groupement attracteur d'électrons sur un carbone voisin de celui sur lequel est fixé le proton diminuera la densité électronique ou le blindage et provoquera la résonance du proton vers les champs faibles (fréquences plus élevées). Et à l'inverse un groupement donneur d'électrons sur un carbone voisin de celui sur lequel est fixé le proton augmentera la densité électronique ou le blindage et provoquera la résonance du proton vers les champs forts (fréquences plus basses).

Le remplacement progressif des hydrogène du méthane par des chlore fait se déplacer la fréquence d'absorption parce que le chlore a tendance à faire diminuer la densité électronique des atomes d'hydrogène.


Tableau 3


Protons du méthane
Nombre d'atome(s) de chlore sur le carbone du méthane Déplacement chimique du (des) proton(s) du méthane (d) Coefficient de corrélation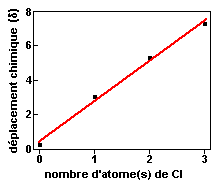
0 0,23 0,9933
1,00 3,05
2,00 5,30
3,00 7,27



Il est aussi intéressant de constater l'effet de substituants de différentes valeurs d'électronégativité comme le montre ce tableau


Tableau 4


Déplacement chimique des protons surdimensionnés (d)
Halogène (X) Électronégativité CH3-X CH3CH2-X CH3CH2CH2-X
F 3,98 4,27 4,36 4,30
Cl 3,16 3,06 3,47 3,30
Br 2,96 2,69 3,37 3,18
I 2,66 2,15 3,16 2,99
coefficient de corrélation 0,9984 0,9918 0,9884




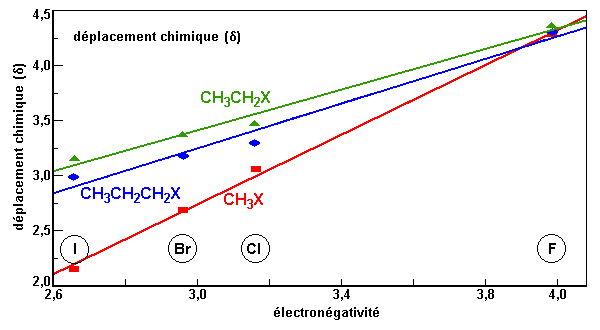
Figure 2.4. Relation entre la valeur d'électronégativité de l'halogène et le déplacement chimique des protons de quelques composés.


La densité électronique est influencée par la résonance aussi bien que par les effets inductifs trouvés dans les alcènes et les composés aromatiques.

Le cas des alcènes peut être illustré par ces deux exemples.

Le crotonate de méthyle a cette structure


Si par comparaison les protons de l'éthène absorbent à 5,28 d, il est tout de suite évident que le proton en A du crotonate de méthyle dont le déplacement chimique est 6,90 d est très déblindé tandis que le proton en B est peu affecté (son environnement électronique est sensiblement le même) par le déplacement des électrons comme on peut le voir sur le schéma.

Dans le cas de l'éther vinylique le mouvement des électrons va dans le sens oxygène vers le méthylène terminal du groupe vinylique. Les protons (H et H) de ce dernier groupe sont donc blindés et leur déplacement chimique est égal à environ 4 d.


L'exemple du trans-anéthole est intéressant puisque s'ajoute dans ce cas l'effet inductif des substituants du noyau aromatique. Le groupe méthoxy possédant un effet inductif positif provoque un déplacement chimique du proton A vers les basses fréquences à presque 6 d.



2.1.4. DÉBLINDAGE PAR DISPERSION DES FORCES DE van der WALLS

Le déblindage d'un proton dans une molécule peut aussi se faire par des forces de dispersion causées par le chevauchement des rayons de van der Walls d'un proton et d'un atome plus électronégatif que l'hydrogène. Très peu de publications ont décrit ce phénomène.

En voici un exemple non publié: le cas de la g,g-diiodolactone décrite en figure 2.6.


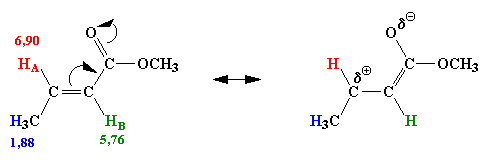
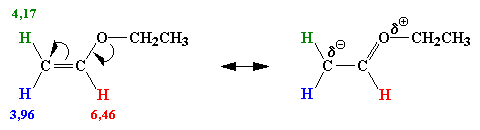
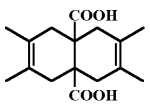
Figure 2.5. Un diacide qui forme une g,g-diiodolactone.


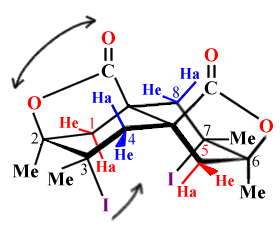Cette iodolactone fut préparée partir du diacide par l'addition d'iode en milieu alcalin. Il est intéressant de noter sur le spectre de RMN de ce composé, le déblindage excessif des méthyles en 3 et 7 par l'iode, qui s'explique par l'effet inductif de ce dernier. Ce déblindage des méthyles s'ajoute à celui des protons en position axiale en 1 et 5 qu'on retrouve à 3,87 d. donc à champ très bas.



Figure 2.6. La dilactone.

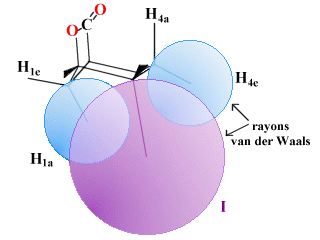Figure 2.7. Le chevauchement des rayons de van der Waals.

En effet l'examen du modèle moléculaire (figure 2.7) montre que les protons 1 et 5 en position axiale sont les plus rapprochés de l'atome d'iode. En outre, l'électronégativité de l'atome d'iode a pour effet d'appauvrir en électrons les atomes de carbone voisins, leur donnant un caractère sp3 plus prononcé; ce qui forcerait les atomes d'iode à "entrer" dans la molécule.

L'infrarouge confirme cette hypothèse en indiquant par une bande g-lactone à 1790 cm-1 l'augmentation de la tension du cycle lactonique (voir figure 2.6). Par comparaison, la fonction lactone de la g,g-dilactone absorbe à 1780 cm-1.

Ce déblindage par l'iode des protons 1 et 5 en position axiale est donc dû à des forces de dispersion causées par le chevauchement des rayons de van der Walls de ces atomes.



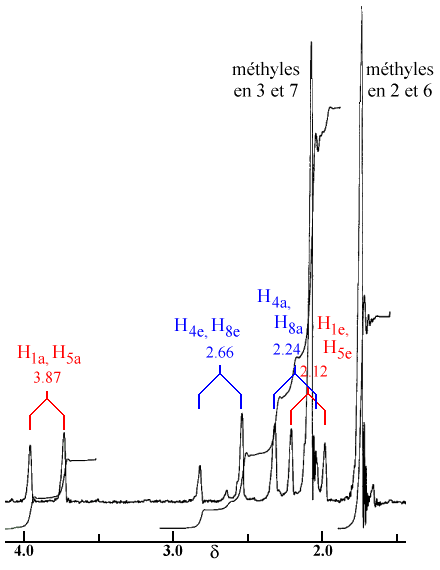
Figure 2.8. Spectre de RMN de la dilactone représentée en figure 2.6. Notez le déblindage des protons 1 et 5 en position axiale et dans une moindre mesure celle des protons 4 et 8 en position équatoriale.



Figure 2.9. Un diacide qui forme une g,d-diiodolactone par deux bandes caractéristiques à 1773 et 1733 cm-1.


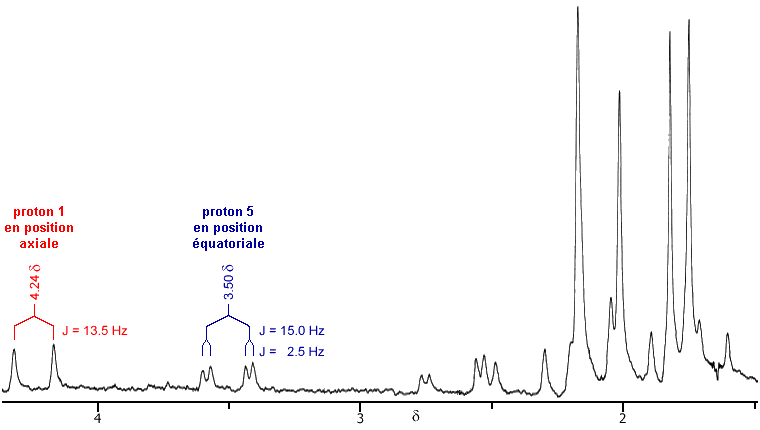
L'iodolactone suivante a été préparée par traitement à l'iode en milieu alcalin comme la g,g-diiodolactone mais à partir du diacide de la figure 2.8. Le spectre infrarouge montre la présence d'une g,d-diiodolactone par deux bandes caractéristiques à 1773 et 1733 cm-1.


On peut voir sur le spectre de RMN que le proton H1 en position axiale est très déblindé à 4.24 d. Le proton H5 en position équatoriale par rapport au cycle d lactonique est aussi très déblindé à 3.50 d ce qui s'explique par la proximité de l'atome d'iode comme dans le cas précédent. Il apparaît sous la forme d'un doublet de doublets couplé avec le proton en axial par une constante de 15 Hz et à longue distance avec le proton H11e par une constante de 2.5 Hz



Figure 2.10. Le spectre RMN qui montre la différence qui existe entre la résonance du proton en 1 et celui en 5.