 Le cabinet de Physique de Sigaud de Lafond
Le cabinet de Physique de Sigaud de Lafond
Notion de la cycloïde. ( Tome 1 page 179)
La perfection du pendule ne répondit point assez bien à l'attente de M. Huygens pour que nous parlions ici de la cycloïde qu'il imagina d'y adapter. Nous laissons à celui qui vaudra traiter cette matière, le soin d'exposer l'idée de ce savant sur l'application de cette courbe au pendule.[..]
Le père Mersenne considérant attentivement le mouvement de l'un des clous appliqués sur l'une des gentes d'une roue de voitures, imagina très bien que ce clou participoit en même tems à deux mouvements ; l'un en ligne droite & l'autre autour de l'arbre de cette roue. D'où il conclut qu'il ne pouvoit décrire une ligne droite, ni une ligne circulaire, mais une courbe qui participoit à la nature de ces deux lignes. Il fit cette belle découverte en 1615 ; mais ce ne fut qu'en 1634, qu'aidé des lumières de Roberval, il parvint à connoître la nature de cette courbe, qu'on appela alors cycloïde, et dont les propriétés ne furent connues que par les travaux du célèbre Descartes et du savant Wren.
Voulez-vous tracer cette courbe mécaniquement ? voici la méthode la plus simple & en même temps la plus exacte. Attachez un crayon sur la circonférence d'un plan circulaire, et perpendiculairement à ce plan. Faites mouvoir circulairement ce dernier sur une ligne droite, & le crayon tracera la cycloïde.
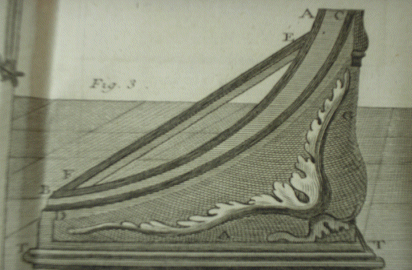
Quatrième Appareil propre à démontrer les propriétés de la cycloïde. ( Tome 1 page 180) Planche .IX bis , fig.3.)
 |
 |
QUATRIEME APPAREIL
Sur un plan AG (Pl.IX bis , fig.3.), on a creusé la gouttière CD , faisant portion d'une cycloïde. On a appliqué à côté une seconde gouttière AB , faisant portion d'une circonférence d'un cercle & une troisième EF, qui représente la corde de cet arc. Le tout est soutenu sur la base TT.
USAGE de cet appareil.
|
On démontre, à l'aide de cet appareil, que si deux billes de métal sont placées, une au haut de la corde EF , & l'autre à l'origine de l'arc AB, & qu'on les abandonne en même temps à elles-mêmes, celle de ces deux billes qui parcourra l'arc AB, arrivera plutôt à la fin de sa chute B, que celle qui descendra le long de la corde EF de cet arc. Si l'on place ces deux billes, l'une au haut de l'arc AB, et l'autre au haut de la gouttière CD, que nous supposons être une portion de cycloïde, aban données en même temps à elles-mêmes, on verra que l'arc cycloïdale sera plus promptement parcouru que l'arc-de-cercle AB. C'est de là que les Mathématiciens ont regardé la courbe cycloïdale comme la ligne de la plus prompte descente. Si au lieu d'un seul arc de cycloïde tel que CD, on creusoit sur un plan deux arcs semblables, l'un à droite & l'autre à gauche, séparés l'un de l'autre à leur points de concours, par une lame de métal, par exemple on observeroit en laissant tomber de part et d'autre deux billes, l'une de toute la hauteur de son arc & l'autre de tout autre point quelconque du sien ; on observeroit, dis-je, que ces deux billes arriveroient en même tems à l'extrémité de leur arc et frapperoient en même tems, la lame qui le sépareroit.
|
 |
D'où il suit que ces deux arcs cycloïdaux de différentes amplitude, sont parcourus dans le même tems, quelque différence qu'il y ait dans leur amplitude. Ce fut cette propriété merveilleuse de la cycloïde, qui fit imaginer à M. Huygens d'appliquer cette courbe au pendule, en faisant osciller celui-ci dans des arcs cycloïdaux ; mais dont comme nous venons de l'observer , le succès ne répondit point à son attente. C'étoit compliquer inutilement la suspension du pendule ; puisqu'il est démontré qu'un arc-de-cercle, comparé à une portion de cycloïde, se confondent sensiblement ensemble vers leurs extrémités inférieures, & que par conséquent on modère également bien le mouvement du pendule, en le faisant osciller dans de très petits arcs-de-cercles, ou entre des lames cycloïdales.
 |
 |
 |
L'appareil est de belle facture, avec un motif floral se détachant sur le fond noir. Il est aussi pratique comme le montre les vis de réglage permettant la mise en position horizontale.
Copyright © 2009 - Contact
Accueil > Instruments > La triple gouttière > Détails