Définition de l’ouverture numérique

Considérons un objectif de microscope observant un point A d'un objet d'indice n_o, recouvert d'une lamelle d'indice n_v, séparée de la lentille frontale de l'objectif par un liquide d'immersion d'indice n. Supposons que le rayon ABCD (fig. 1) soit le rayon le plus incliné sur l'axe optique, capable d'entrer dans l'objectif et d'en ressortir. Son inclinaison à la traversée des dioptres plans séparant les milieux prend les valeurs successives u_o, u_v, U  tels que

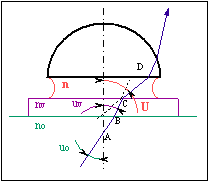
Fig. 1

Cette quantité invariante n sin U est l'ouverture numérique de l'objectif. Plus encore que son grandissement, cette grandeur est sa caractéristique principale. Outre qu'elle régit la quantité de lumière entrant dans l'instrument, c'est elle qui définit sa profondeur de champ et sa propriété la plus essentielle : sa limite de résolution.

Ouverture numérique et limite de résolution de l’objectif

Doter l’objectif d'un grandissement suffisamment fort pour agrandir l'image n'est pas suffisant. Il est encore nécessaire, à l'intérieur des limites de l'objet, de résoudre ses détails. La limite de séparation entre deux points habituellement utilisée n'est pas vraiment significative pour définir la qualité d'un objectif de microscope destiné à l'observation d'objets étendus.

En microscopie, de même qu'en photographie et en astronomie (hormis l'observation des étoiles), on peut considérer que l'objet, telle une photographie tramée, est constitué d'une structure analogue à un ensemble d'objets périodiques de fréquences « spatiales », de contrastes et d'orientations différents. La limite de résolution de l'objectif est alors définie comme étant la plus petite période résolue par l'objectif. Cette limite de résolution varie selon les dimensions de la source éclairant le champ du microscope.

Considérons un objet ne présentant dans une direction que des variations de transmission purement sinusoïdales de période spatiale p. Immergé dans un milieu d'indice n, éclairé par une onde plane _i émise par une source ponctuelle S placée au foyer d'un condenseur C_d (fig. 2), il se comporte comme un réseau diffractant la lumière de longueur d'onde dans deux directions symétriques inclinées sur l'axe d'angles tel que

Fig. 2

Tant que reste inférieur à U, angle d'ouverture objet, il existe deux ondes ₁ et ₂ diffractées par le réseau. L'ensemble condenseur-objectif fournit dans le plan de la pupille de sortie P'_o de l'objectif deux images de la source S₁ et S₂ centres de deux ondes sphériques '₁ et '₂ cohérentes entre elles, reconstruisant par interférence une image conforme de l'objet. La limite de résolution est, en éclairage cohérent, la période p_c (fig. 5) telle que

et, pour toute fréquence spatiale 1/p inférieure l'image obtenue est de contraste unité alors que les fréquences spatiales supérieures ne sont pas transmises. Notons que plus généralement, un objet périodique spatialement est décomposable en un ensemble de composantes sinusoïdales fournissant chacune une paire d'ondes diffractées reconstruisant une image conforme tant qu'elles sont transmises par la pupille. À la limite, si seules les ondes correspondant à la fréquence spatiale /p la plus basse, c'est-à-dire la fréquence fondamentale de l’objet, sont transmises par la pupille, l'image reconstruite par interférences est purement sinusoïdale.

Inversement, si la source est infiniment étendue (éclairage incohérent), elle est néanmoins limitée par l'image dans son plan de la pupille de sortie P'_o. L’objet sinusoïdal en intensité fournit une onde directe remplissant toute la pupille et deux ondes diffractées formant dans ce plan deux images S₁ et S₂ de la source (fig. 3). Dans les zones communes à deux de ces ondes existent des points homologues donnant naissance à des systèmes d'interférences identiques reconstruisant une image de l'objet.

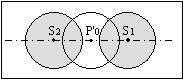
Fig. 3

Il y a perte d'énergie et le contraste, proportionnel à l'aire commune aux cercles S₁-P'_o et S₂-P'_o, diminue quand la fréquence spatiale augmente et s'annule (fig. 5) lorsque les images S₁ et S₂ sont tangentes extérieurement à P'_o pour une fréquence spatiale :

La période correspondante pi constitue la limite de résolution absolue de l’objectif :

Le contraste pour les faibles fréquences spatiales peut être augmenté - ce qui est constaté depuis fort longtemps par les microscopistes utilisant couramment cette procédure - en réduisant l'ouverture numérique du condenseur à une valeur n sin u_c inférieure à celle de l'objectif à l’aide d’un diaphragme d'ouverture D_o dont l'image dans le plan de la pupille de l'objectif est plus petite que cette pupille (fig. 4).

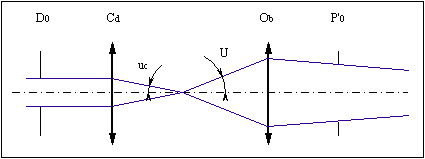
Fig. 4

Par un raisonnement analogue aux précédents, on voit que, avec cet éclairage partiellement cohérent, le contraste de l'image (fig. 5) reste égal à l'unité tant que

et s'annule pour une limite de résolution p_s telle que

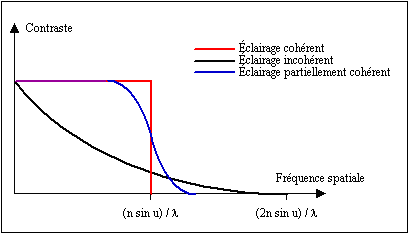
Fig. 5

La limite de résolution est donc d'autant meilleure que l'ouverture numérique est grande, ce qui justifie l’immersion éventuelle de l’objet pour l’augmenter aux grandissements les plus forts. S’il existe des objectifs à sec (n = 1) d'ouverture atteignant 0,95 d’angle U égal à 72°, de limite de résolution absolue égale à 0,3 µm, l'immersion homogène (l’indice n = 1,518 étant celui de la lamelle couvre-objet et de la lentille frontale) permet des résolutions inférieures à 0,2 µm pour une ouverture de 1,25 d’angle U  égal à 55°.

L’ouverture numérique ne détermine pas seulement la limite de résolution de l’objectif du microscope. Elle conduit aussi à une limitation du grossissement commercial du microscope et définit à la fois la profondeur de champ de l’objectif et la latitude de mise au point du microscope.

Le microscope, instrument associé à l’œil

Le microscope est un instrument associé à l'œil d'un observateur formant l'image définitive. La performance acquise par l’objectif grâce à sa limite de résolution ne doit donc pas être réduite par la limite de perception de l'œil. Or celle-ci varie en fonction de la luminance du champ et pour les luminances moyennes rencontrées en microscopie : la limite de perception est optimale si la pupille de l’œil est diaphragmée à un diamètre o compris entre 0,5 et 0,8 mm. Dans ces conditions, la pupille de sortie du microscope ' (fig. 6) doit avoir un diamètre

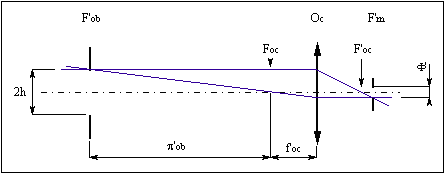
Fig. 6

puisque h / f'ob = n sin U, si ' est exprimé en millimètres et en appliquant les formules de conjugaison dites de Newton particulièrement bien adaptées au microscope où la distance '_ob est normalisée pour respecter la correction des aberrations des objectifs et des oculaires.

Le grossissement optimum du microscope G_M doit donc vérifier la double inégalité

Le choix du grossissement ne s'effectue donc pas en choisissant le grandissement de l'objectif et le grossissement de l'oculaire, mais en fonction de la résolution souhaitée, déterminée par l’ouverture numérique de l’objectif, ce qui conduit aux compositions maximales limites idéales :

Compte tenu de la forte valeur des angles d’ouverture dans l’espace objet (de 15 à 60°), les conditions de l’approximation de Gauss ne sont plus satisfaites et ses propriétés ne peuvent être utilisées pour vérifier la conservation du stigmatisme dans un plan perpendiculaire à l’axe optique et le long de celui-ci.

L'objectif de microscope doit former une image d'un objet situé dans un plan perpendiculaire à son axe optique. Stigmatique pour un couple de points objet-image A-A' situés sur l'axe, il doit également l'être pour un couple de points B-B' infiniment voisins situés dans des plans perpendiculaires à l'axe (fig. 7). S'il respecte ces conditions, l'objectif est dit aplanétique et il satisfait à la condition d'Abbe ou condition des sinus qui, l'angle d'ouverture image étant faible et si le milieu intermédiaire est l'air, peut s’écrire :

n y sin u = y' u'

n étant l’indice de réfraction du milieu objet, y et y' les grandeurs de AB et A'B', u et u' les inclinaisons sur l'axe d'un même rayon lumineux quelconque passant par les points A et A'.

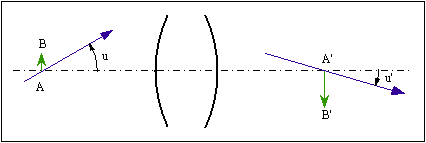
Fig. 7

Dans le cas de l’objectif de microscope, le point objet stigmatique A_o est très proche de son foyer objet et l’on peut admettre que la condition d'aplanétisme s'écrive alors :

n f'_ob = h / sin u

où (fig. 8) la hauteur pupillaire h est la distance à l'axe du rayon émergent correspondant à un rayon incident passant par A_o d'inclinaison u.

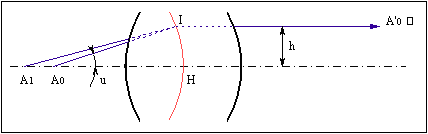
Fig. 8

La quantité h / sin u étant constante, la surface principale, lieu du point d'intersection I des rayons incident et émergent correspondants, est une sphère de rayon n f'_ob centrée en A_o. La différence des chemins optiques parcourus le long de deux rayons quelconques entre A_o et tout point de cette sphère étant nulle, le chemin optique entre A_o et son image à l'infini est conservée, ce qui exprime la condition de stigmatisme. Cette sphère principale peut être assimilée à une surface d'onde issue du point A_o considéré comme source lumineuse ponctuelle. Pour un second point objet A₁ situé sur l'axe optique à la distance _z de A_o, on admet que la condition de stigmatisme se conserve si la différence entre les chemins optiques parcourus le long des rayons A₁I et A₁H appelée différence de chemin optique aberrant, H étant sur l'axe, est inférieure à /4, critère suffisant pour que la correction des aberrations ne soit pas affectée et qu’ainsi la qualité de l'image reste acceptable. Cette condition fixe la valeur maximale du défaut de mise au point tolérable pour un objectif d'ouverture numérique n sin U

Cette faible quantité peut être considérée comme une limite de résolution longitudinale.

En ce qui concerne la latitude de mise au point du microscope, l'objectif et l’oculaire étant rigidement liés, il n’est donc pas possible d’en dépointer l'ensemble par rapport au plan du point stigmatique A_o (fig. 9) d'une quantité supérieure à cette limite.

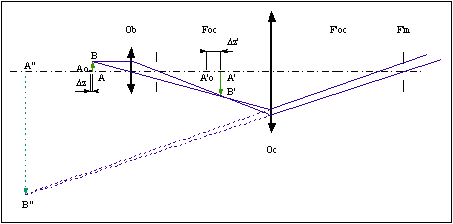
Fig. 9

On ne peut donc tolérer un décalage de l’image intermédiaire A'B' par rapport au plan focal objet de l'oculaire déterminé par un raisonnement analogue au plus égal à

Pour un tel décalage, l'image définitive A"B" n'est plus à l'infini et sa distance à l'anneau oculaire du microscope est la plus courte distance d'accommodation permise. En négligeant la distance de l'anneau oculaire au plan focal image de l'oculaire devant la distance d'accommodation et par application de la formule de conjugaison de Newton, on en déduit la puissance d'accommodation P_ac, inverse de la distance d’accommodation :

Il en résulte, en admettant que la puissance du microscope soit celle pour laquelle son grossissement optimal est maximum, une puissance d’accommodation tolérable maximale

Au delà de cette limite, il est préférable que les observateurs fortement amétropes conservent leurs verres correcteurs pour l'observation, ce qui est facilité par l’existence d’oculaires à pupille de sortie éloignée spécialement conçus pour porteurs de lunettes.